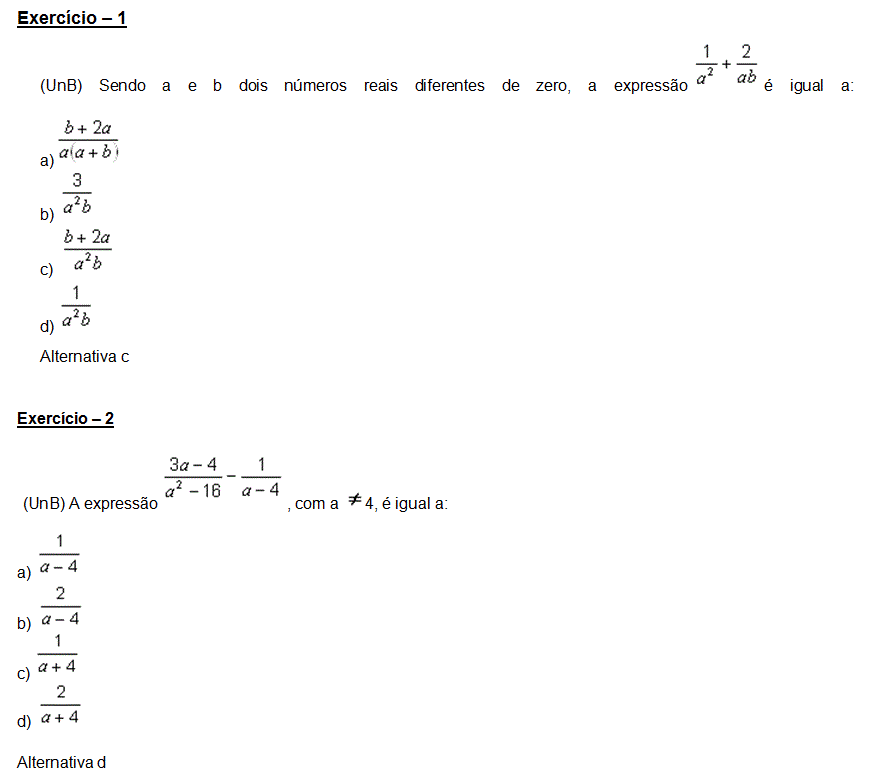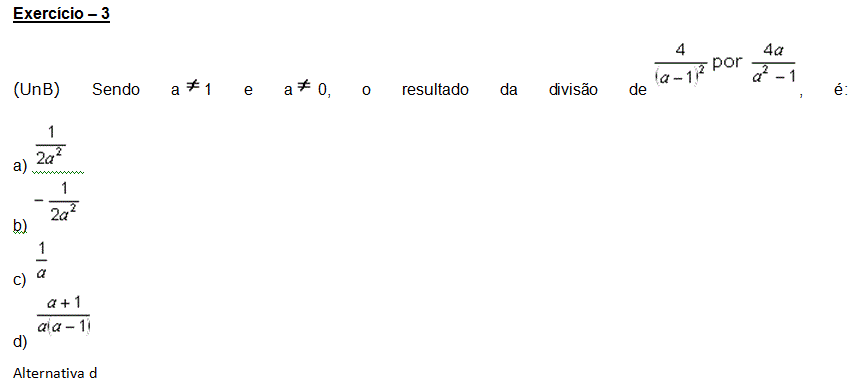Neste post serão definidas as frações algébricas, suas operações e simplificações. Estes conceitos facilitam o tratamento com expressões deste tipo. Aproveite esta aula e se garanta para matemática no Enem!
Frações algébricas: uma expressão algébrica é usada para representar uma constante, uma variável ou uma combinação de variáveis e constantes relacionadas por um número finito de operações (adição, subtração, multiplicação, divisão, radiciação, potenciação). Complicou para você compreender partindo assim da definição clássica? Então, pode se tranquilizar, que vamos descomplicando etapa por etapa para você aprender as frações algébricas.
Frações Algébricas
Para começo de conversa, uma ‘fração’ significa uma parte de um todo. Por exemplo 1/4 (um quarto) tem a significação direta de 0,25. Temos, então: 1/4 = 0,25
Mas, na fração algébrica temos no denominador pelo menos uma incógnita a ser desvendada (para ser resolvida). Então, a nossa fração algébrica, partindo do exemplo inicial de fração, seria, por exemplo 1/x = 0,25. E, a incógnita a ser descoberta ao resolver a conta é o ‘x’ da questão. Neste caso, x = 4
Esse tipo de expressão é muito utilizado na geometria, por exemplo, para representar áreas, perímetros e volumes de figuras ou objetos que possuem dimensões algébricas.
Veja uma síntese sobre as frações algébricas e as regras que precisam ser respeitadas para que a equação seja válida e que possa ser resolvida. O denominador (a parte de baixo) nunca pode ser zero, pois não há divisão por zero.
Confira:

Obs.: As operações de adição, subtração, multiplicação e potenciação de frações algébricas são exatamente iguais às operações realizadas com frações não algébricas. A seguir trazemos alguns exemplos:
Adição e Subtração
Tanto na adição como na subtração de frações, devemos obter o m.m.c. dos denominadores. Exemplos: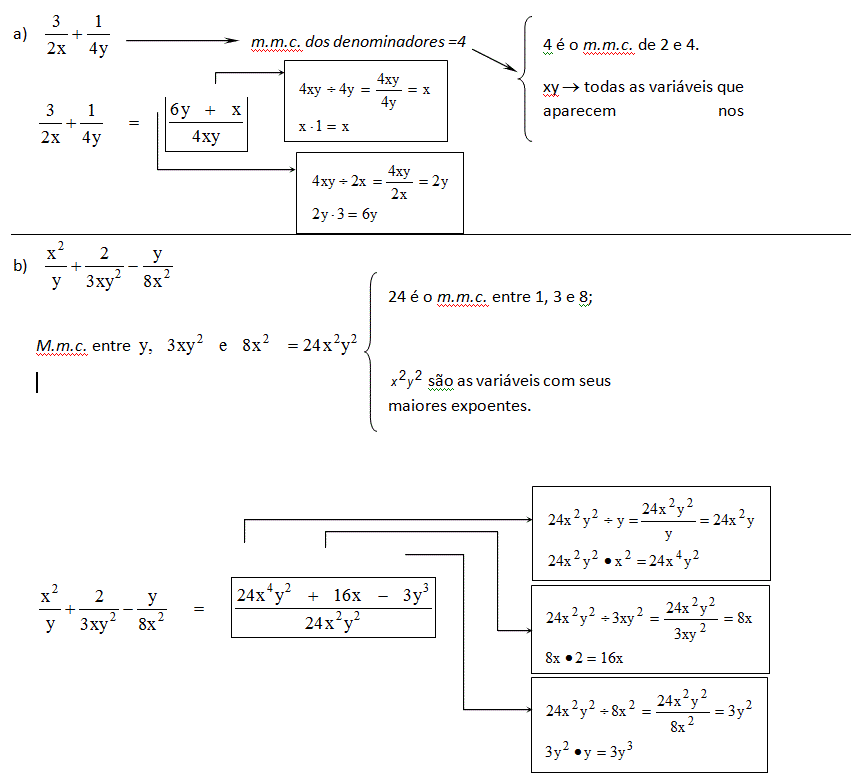
Qual a diferença entre m.d.c. e m.m.c.?
M.D.C: é o mínimo divisor comum. Usado quando determinamos fatores comuns (aquilo que aparece em todos os termos) para colocar em evidência.
Ex.: a) 2, 4, 6 Þ m.d.c. é 2, pois 2 é o menor número que divide 2, 4 e 6.
b) 10, 15, 20 Þ d.c. é 5, pois 5 é o menor número que divide 10, 15 e 20.
M.M.C: é o Mínimo múltiplo comum. Usado quando somarmos ou subtrairmos frações.
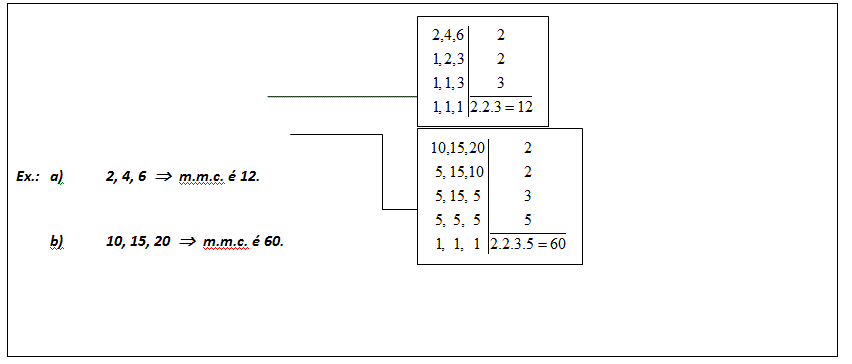
Qual é o mmc de 2,4 e 6 ?
Observe:
múltiplos de 2 : 2,4,6,8,10,12,14,16,18,…. (como se fosse a tabuada do 2)
múltiplos de 4 : 4,8,12,16,20,24,28,32,…..(como se fosse a tabuada do 4)
múltiplos de 6 : 6,12,18,24,30,36,,………..(como se fosse a tabuada do 6)
O número 12 é o menor dos múltiplos de 2, 4 e 6 por isso é chamado de mínimo múltiplo comum.(mmc).
No entanto não é necessário recorrer a este modo para determinar o mmc de vários números. Pode-se usar a regra prática de decomposição simultânea em fatores primos.
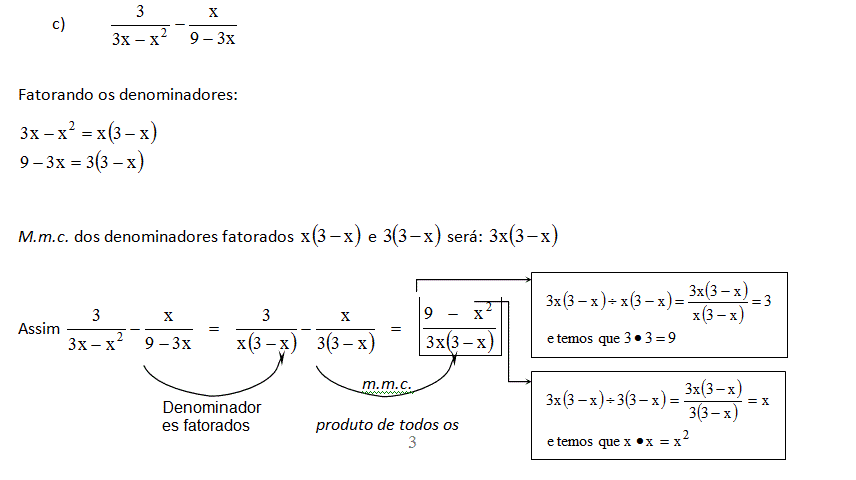
Nos exemplos “c” e “d” a seguir, para obter o mmc dos denominadores teremos que escrevê-los na forma fatorada.

Dica 1: Veja também as notações científicas com esta super aula da professora Jaceli: https://blogdoenem.com.br/notacao-cientifica-matematica-enem/
Multiplicação e divisão de frações algébricas
A multiplicação e divisão de frações algébricas é exatamente igual a de frações numéricas, ou seja não é necessário obter o mmc dos denominadores. Multiplica-se numerador por numerador e denominador por denominador.
Exemplos:
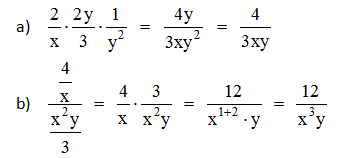
Veja a videoaula do prof. Sarkis que explica de maneira simples as expressões algébricas: