Veja como transformar números decimais em frações. Esta parte da matemática causa muita confusão na hora da resolução das questões. Mas, é simples para aprender:
Os números decimais são largamente utilizados em nosso dia-a-dia, e caem direto no Enem. Vejamos uma situação: Se formos ao supermercado comprar 1 kg de batatas por R$ 1,32 e pagarmos a compra com uma nota de R$ 2,00, receberemos R$ 0,68 de troco.
Neste exemplo, podemos observar a utilização dos números decimais. Veja como transformar esses números decimais em frações:
Decimais finitos: São aqueles que apresentam um número finito de casas decimais não nulas. Observe que:
1) 7/10 = 0,7
2) 7/100 = 0,07
3) 7/1000 = 0, 007
4) 216/100 = 2,16
Todo número cuja representação decimal for finita pode ser escrito na forma de uma fração com denominador 10, 100, 1000, etc. Os números que mais lidamos são os decimais, por isso saber operá-los é muito importante para que não haja perdas significativas em nosso orçamento, por exemplo.
Resumo sobre números decimais
Confira com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito, um resumo rápido sobre Números Decimais:
Viu que show esta aula do professor Sarkis, com as dicas ele te explica tudo sobre os números decimais! 😀
Entenda agora as Frações
O numerador da fração é o número inteiro que se obtém abandonando a vírgula e o denominador é formado pelo número 1 acrescido de tantos zeros quanto forem as casas após a vírgula do número fornecido. Tá complicado? Vamos simplificar para você dominar bem este tema.
Para começo de conversa, uma ‘fração’ significa uma parte de um todo. Por exemplo 1/4 (um quarto) tem a significação direta de 0,25. Temos, então: 1/4 = 0,25
Mas, na Fração Algébrica temos no denominador pelo menos uma incógnita a ser desvendada (para ser resolvida). Então, a nossa Fração Algébrica, partindo do exemplo inicial de fração, seria, por exemplo 1/x = 0,25. E, A incógnita a ser descoberta ao resolver a conta é o ‘x’ da questão. Neste caso, x = 4
Esse tipo de expressão é muito utilizado na geometria, por exemplo, para representar áreas, perímetros e volumes de figuras ou objetos que possuem dimensões algébricas.
Veja uma síntese sobre as Frações Algébricas e as regras que precisam ser respeitadas para que a equação seja válida e que possa ser resolvida. O denominador (a parte de baixo) nunca pode ser zero, pois não há divisão por zero.
As frações são constituídas de duas partes, o numerador e denominador:
Uma fração é uma maneira de representar um número por uma divisão, na qual o numerador está sendo dividido pelo denominador.
Somar frações quando o denominador é igual é muito fácil, acompanhe:
Viu? – É simples demais, se o denominar é comum a todas as frações basta somar os numeradores e copiar o denominador, que está prontinho.
Resumo sobre Frações e Números Decimais
Que a matemática é tida como um monstro na vida da maioria dos(das) estudantes, principalmente de quem está se preparando para o vestibular e Enem, não é novidade. Mas, a parte divertida e que muitas vezes não é ensinada na sala de aula é a possibilidade de adaptação dos conteúdos.
Um bom exemplo são os números decimais: tem estudantes que gostam mais de trabalhar com “números com vírgula” e outros que preferem trabalhar com frações. A mágica acontece quando você percebe que basta transformar números decimais em frações, ou vice e versa, para estudar da forma que você preferir. Veja no resumo gratuito:
Entendeu como se transforma uma fração em um número decimal? Que tal você nunca mais esquecer isto? Assista a duas videoaulas da Khan Academy, traduzido para o Português pela Fundação Lemann, onde o professor Salman Khan da exemplos de como fazer essa transformação. Saia na frente!
Dica 1 – O que mais cai em Matemática nos Vestibulares e no Enem? Veja aqui as melhores dicas: https://blogdoenem.com.br/category/cainaprova/matematica/
Dica 2 – Estude também as operações envolvendo os números na forma decimal. Acesse o nosso link e fique por dentro! https://blogdoenem.com.br/operacoes-decimal-matematica-enem/
Aula disponível também na plataforma da Khan: https://goo.gl/lzcTWu
Veja agora as Dízimas Periódicas
Dízimas periódicas: São numerais decimais em que há repetição periódica e infinita de um ou mais algarismos.
Observe as divisões:
1) 5/9 = 0,55555….
2) 32/99 = 0,32323232…
3) 121/999 = 0,121121121…
Note que estes números têm uma representação decimal infinita e periódica e são chamados de dízimas periódicas simples. A fração que os representa (Fração Geratriz) tem como denominador números 9.
Podemos estabelecer a seguinte regra para dízimas periódicas simples: o numerador da fração geratriz será o número do período e o denominador será 9 ou 99 ou 999, etc…, ou seja, será formado por tantos nove quanto forem os algarismos do período.
Exemplos de dízimas periódicas:
1) 0,454545… = 45/99
2) 0,761576157615… = 7615/9999
3) 0,222222… = 2/9
E se o número for, por exemplo, 2,3222222…. ou 0, 43717171…?
Neste caso será chamado de dízima periódica composta e a sua transformação em fração pode ser feita da seguinte maneira:
Exemplos:
1) 2,3222222… =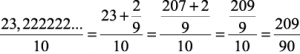 
2) 0,43717171… =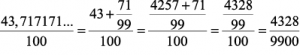
Revise mais sobre a transformação dos números decimais em frações assistindo a videoaula do Guto. Nesse vídeo você aprende em apenas cinco minutos e vinte e cinco segundos, tudo sobre esse assunto bastante cobrado em diversas provas do Enem e dos vestibulares de todo Brasil. Não deixe essa chance passar!
Dica 3 – Matemática Enem – revise os Múltiplos e Divisores – https://blogdoenem.com.br/multiplos-e-divisores-enem/
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
1) No tanque do seu carro cabem 50 litros de gasolina. Num certo momento, o marcador indica que ainda resta 1/4 do tanque. Se você quiser completar, quantos litros de gasolina deverá comprar? Se a gasolina custa R$2,58 o litro, quanto você pagará para completar o tanque?
Resposta: 37,5 litros e R$ 96,75 para completar o tanque.
Dica 4 – Relembre outros assuntos de matemática acessando o nosso blog www.blogdoenem.com.br e gabarite as questões de matemática nas provas dos vestibulares e do Enem.
