Trapézios, Retângulos, Quadrados, e Losangos - Veja a classificação e as principais propriedades dos Quadriláteros. Estas Figuras Geométricas caem sempre no Enem, nos vestibulares e no Encceja!
Nesta aula de Matemática Básica serão abordados tópicos referentes à definição de um Quadrilátero; a Classificação dos Quadriláteros e suas Propriedades. Acompanhe esta aula e garanta um excelente resultado em Matemática no Enem, nos vestibulares e no Encceja!
O que são os Quadriláteros?
Os quadriláteros são as figuras mais utilizadas na criação de estruturas e outros objetos que nos cercam, como por exemplo:
– na fachada de um edifício;
– na construção de uma quadra de tênis;
– em estruturas de telhados e coberturas;
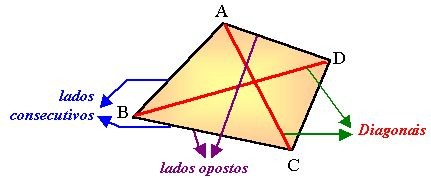
– em obras artísticas, etc. O paralelogramo abaixo é um Quadrilátero: 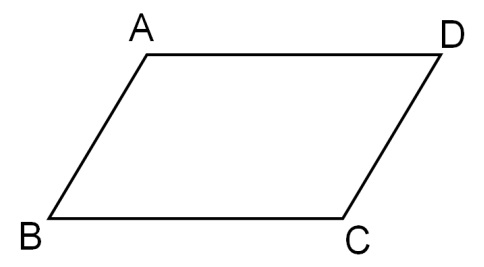
Um Quadrilátero, portanto, é a figura formada por quatro pontos A, B, C e D no plano acima, pelos vértices dos quatro ângulos, e pelos segmentos (lados) que os unem.
Para você não esquecer – Um quadrilátero tem:
- 4 lados – [AB] , [BC] , [CD] , [DA] ;
- 4 vértices – A , B , C , D ;
- 4 ângulos – CBA , DCB , ADC , BAD;
- [AC] e [BD] são as diagonais.
- Veja na imagem com calma, e leia novamente estes tópicos para compreender e lembrar sempre.

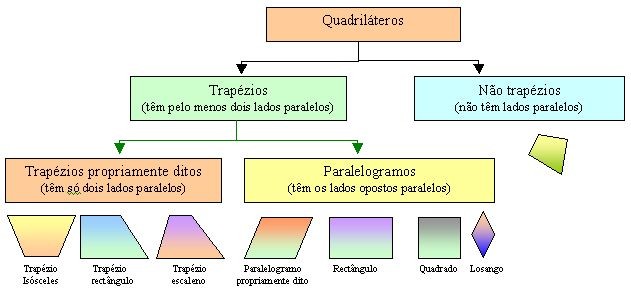
A Classificação dos quadriláteros:
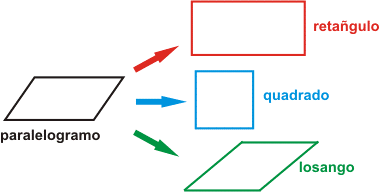
- Paralelogramo >>> quatro lados paralelos dois a dois
- Trapézio >>> dois lados paralelos e dois não paralelos.
A Classificação dos paralelogramos:
- retângulo >>> quatro ângulos retos e lados diferentes
- quadrado >>> quatro ângulos retos e lados iguais
- losango >>> ângulos agudos e obtusos e lados iguais.

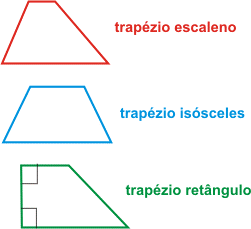
A Classificação dos trapézios:
- escaleno >>> lados não paralelos diferentes.
- isósceles >>> lados não paralelos iguais
- retângulo >>> dois ângulos retos

Aula Gratuita: Cálculo de Área e de Perímetro
Veja um resumo simples e rápido com o professor Sérgio Sarkis, do canal Curso Enem Gratuito, para você aprender a fazer os cálculos mais importantes dos quadriláteros. Área e Perímetro sempre caem nas provas.
Muito bom este resumo. Veja agora mais dicas sobre os Quadriláteros:
A Diagonal de um quadrilátero é o segmento de reta que une dois vértices não consecutivos.
O quadrilátero possui 2 diagonais.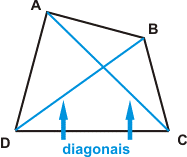
A Base de um paralelogramo é um de seus lados, normalmente é o maior lado.
A base de um trapézio é um de seus lados paralelos, normalmente o maior.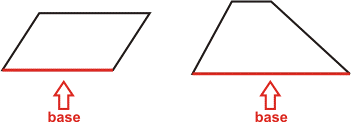
A Altura de um quadrilátero é a distância entre dois lados paralelos.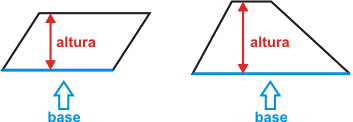
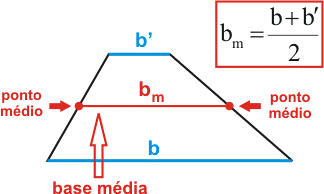
Obs.: Base média de um trapézio é o segmento de reta que une os pontos médios dos lados não paralelos.
A base média é paralela à base do trapézio e seu valor é igual à média aritmética das medidas das bases.
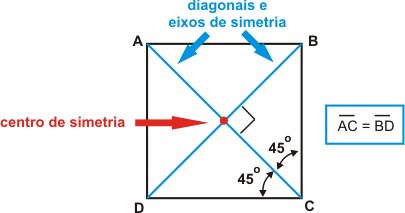
Propriedades do quadrado:
- as diagonais são iguais
- as diagonais são ortogonais
- as diagonais são bissetrizes dos ângulos internos
- as diagonais são eixos de simetria
- as diagonais cortam-se no ponto médio que é um centro de simetria.

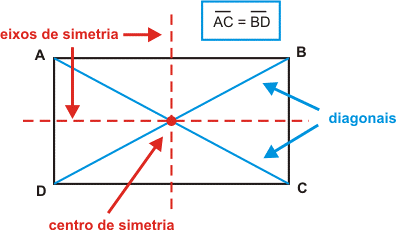
As Propriedades do Retângulo:
- as diagonais são iguais
- o retângulo tem dois eixos de simetria
- as diagonais cortam-se no ponto médio que é um centro de simetria.

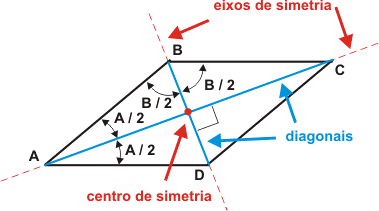
As Propriedades do Losango:
- as diagonais são ortogonais
- as diagonais são bissetrizes dos ângulos internos
- as diagonais são eixos de simetria
- as diagonais cortam-se no ponto médio que é um centro de simetria.

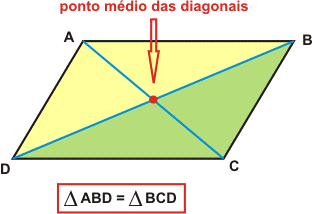
As Propriedades dos Paralelogramos:
- as diagonais cortam-se no ponto médio
- cada diagonal divide o paralelogramo em dois triângulos iguais.

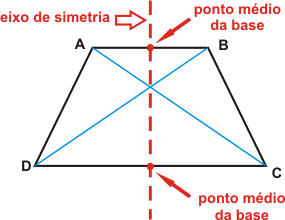
Propriedade do trapézio isósceles:
- a reta que passa pelos pontos médios das bases é um eixo de simetria

Quadro Resumo da Classificação dos quadriláteros
Assista a aula que foi selecionada para esclarecer as suas dúvidas sobre as propriedades dos quadriláteros!
Exercício – 1 (Ufrs 2004) A opção que apresenta todas as possibilidades do número de pontos de interseção de um círculo com um retângulo é
a) 0, 1, 2, 4 ou 8.
b) 0, 2, 4, 6 ou 8.
c) 0, 1, 3, 5 ou 7.
d) 0, 2, 3, 5 ou 7.
e) 0, 1, 2, 3, 4, 5, 6, 7 ou 8.
Alternativa e
Exercício – 2 (Fuvest 2000) Um trapézio retângulo tem bases 5 e 2 e altura 4. O perímetro desse trapézio é:
a) 13
b) 14
c) 15
d) 16
e) 17
Alternativa d
Exercício – 3 (Puc-rio 99) ABCD é uma paralelogramo, M é o ponto médio do lado CD, e T é o ponto de intersecção de AM com BD. O valor da razão DT/BD é:
a) 1/2.
b) 1/3.
c) 2/5.
d) 1/4.
e) 2/7.
Alternativa b