Você também acha Trigonometria difícil? Que nada, vem revisar com o blog do Enem. Aprenda a utilizar o Círculo Trigonométrico, entenda os Quatro Quadrantes, e fique afiado para a prova de Matemática do Enem ou dos Vestibulares!
Nos estudos trigonométricos existem arcos que possuem medidas maiores que 360º, isto é, eles possuem mais de uma volta e são conhecidos como arcos côngruos.
Neste post, serão tratados os métodos para reduzir um arco ao 1º quadrante e consequentemente um arco côngruo a outro. Confira!
Arcos Côngruos e primeira determinação positiva:
Para começar esta aula de Arcos Côngruos é fundamental que você observe com calma esta representação do Círculo Trigonométrico. Nele, temos que uma volta completa no círculo trigonométrico corresponde a 360º ou 2π rad.
Veja na ilustração a seguir para ir construindo o seu aprendizado. Presta atenção: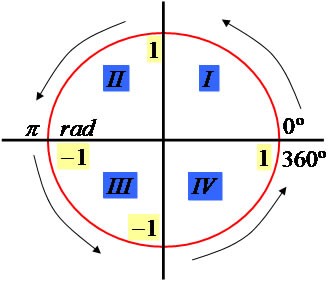
Note que o círculo possui raio medindo uma unidade e é dividido em quatro quadrantes, facilitando a localização dos ângulos trigonométricos, de acordo com a seguinte situação: 
1º quadrante: abscissa positiva e ordenada positiva → 0º < α < 90º.
2º quadrante: abscissa negativa e ordenada positiva → 90º < α < 180º.
3º quadrante: abscissa negativa e ordenada negativa → 180º < α < 270º.
4º quadrante: abscissa positiva e ordenada negativa → 270º < α < 360º.
Resumo sobre o Ciclo Trigonométrico
Aprenda agora na aula bem didática do professor Lucas Borguesan, do canal do Curso Enem Gratuito, para você dominar de maneira prática os segredos do Cíclo Trigonométrico:
As dicas sobre o Cíclo Trigonométrico:
- O ciclo trigonométrico é um círculo de raio 1. Ou seja, do seu cento até a borda, a medida é 1.
- Assim, podemos definir todos os valores de seno e cosseno que existem, uma vez que o círculo trigonométrico compreende todos os ângulos.
- Na trigonometria, seno e cosseno são chamados de razões trigonométricas.
- Para medir o valor do seno, é comum usar o eixo vertical do círculo trigonométrico. Desta forma, o eixo vertical do ciclo trigonométrico é chamado eixo dos senos.
- Por outro lado, podemos encontrar o valor do cosseno no eixo horizontal, de maneira que este é chamado de eixo dos cossenos.
- Veja novamente o resumo acima, para você dominar e mandar bem no Enem.
Entenda os 360 Graus do Ciclo Trigonométrico
Sabemos que uma volta completa equivale a 360º ou 2π rad, com base nessa informação podemos reduzi-lo à primeira volta, realizando o seguinte cálculo: dividir a medida do arco em graus por 360º (volta completa).
O resto da divisão será a menor determinação positiva do arco. Dessa forma, a determinação principal do arco em um dos quadrantes fica mais fácil.
- Exemplo 1
Determinar a localização principal do arco de 4380º utilizando a regra prática. - 4380º : 360º é correspondente a 4320º + 60º, portanto, o resto da divisão é igual a 60º que é a determinação principal do arco, dessa forma, sua extremidade pertence ao 1º quadrante.
- Exemplo 2
Qual a determinação principal do arco com medida igual a 1190º? - 1190º : 360º, a divisão possui resultado igual a 3 e resto 110, concluímos que o arco possui três voltas completas e extremidade no ângulo de 110º, pertencendo ao 2º quadrante.
Tá difícil? Veja uma aula introdutória?
Veja com o professor Sérgio Sarkis um resumo simples e rápido com o básico da Trigonometria antes de continuar. Confira como ele explica enquanto resolve exercícios simples do Encceja:
Viu como um resumo bem simples muitas vezes ajuda? Vamos continuar.
Veja os Arcos Côngruos
Definição: Dois arcos são côngruos quando possuem a mesma origem e a mesma extremidade. Uma regra prática eficiente para determinar se dois arcos são côngruos consiste em verificar se a diferença entre eles é um número divisível ou múltiplo de 360º.
Isto significa que a diferença entre as medidas dos arcos dividida por 360º precisa ter resto igual a zero.
- Exemplo 3
Verifique se os arcos de medidas 6230º e 8390º são côngruos. - 8390º – 6230º = 2160
2160º / 360º = 6 e resto igual a zero. Portanto, os arcos medindo 6230º e 8390º são côngruos.
- Exemplo 4
Confira se os arcos de medidas 2010º e 900º são côngruos. - 2010º – 900º = 1110º
1110º / 360º = 3 e resto igual a 30. Portanto, os arcos não são côngruos.
Dica do Blog: Quer ficar ‘uma fera’ no Círculo Trigonométrico, e gabaritar nas questões mais avançadas de Seno e Cosseno nas questões de Matemática? Veja na imagem uma aula completa, gratuita: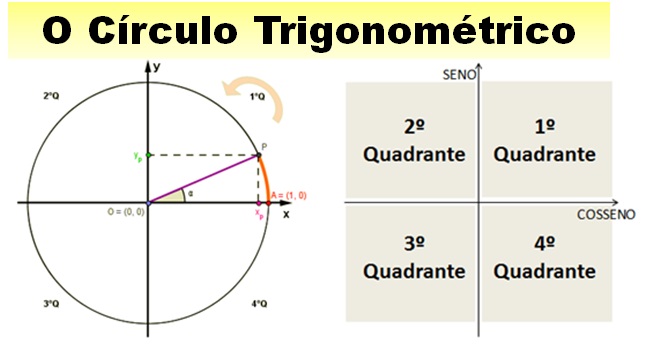 
Chega de ter medo das questões de Trigonometria. Dá sim para aprender e mandar bem. Confira acima.
Forma Geral dos Arcos Côngruos
Todos os arcos no círculo trigonométrico possuem determinações, isto é, tem origem e extremidade. Dois ou mais arcos podem ter a mesma determinação, mas não podemos garantir que eles possuam o mesmo comprimento, pois ocorre que eles podem possuir um número inteiro de voltas completas diferentes.
Nesse caso devemos aplicar uma definição geral para representar arcos e todos os seus côngruos.
Se um arco mede α graus, podemos expressar todos os arcos côngruos a ele da seguinte forma: α + 360º*k, k ? Z. Caso a medida do ângulo do arco seja dada em radianos, representamos por: α + 2π*k, k ? Z.
A determinação principal de um arco que mede α (graus ou radianos) é dada de acordo com as definições: 0º ≤ α < 360º ou 0 ≤ α < 2π. No caso de um ângulo maior que 360º devemos realizar a divisão por 360º e considerar o resto o valor da determinação principal.
O resultado da divisão mostrará quantas voltas o arco realizou. Observe nos exemplos a seguir:
Exemplo 5: Considerando o arco α = 2100º, qual será a sua determinação principal.
2100º : 360º = quociente 5 e resto igual a 300. Portanto, o arco possui determinação principal no 4º quadrante (300º), com 5 voltas completas.
Exemplo 6: Dado o arco 17π/4 rad, a sua determinação principal será:
17π/4 rad = 16π/4 + π/4 = 4π + π/4, onde:
4π = corresponde a duas voltas completas
π/4 = determinação principal (45º – 1º quadrante)
E aí, ficaram prontos para resolver as questões sobre os arcos côngruos na matemática do Enem?
Não, então confira a aula que traz um exercício para calcular a 1ª determinação positiva de um ângulo. Não esqueça de resolver os exercícios. Boa sorte!
Exercício – 1
(UNISINOS) Marcar no círculo trigonométrico as extremidades dos arcos de medidas x=2k/3, onde k é um número inteiro.
R: 2π
Exercício – 2
(FEI) Calcule a primeira determinação positiva do conjunto de arcos de mesma extremidade que o arco de medida 38/3Parte superior do formulário.Parte inferior do formulário
R: 2/3
Exercício – 3
(FEI) Quantos são os valores de m compreendidos entre 30 e 40, que tornam côngruos os arcos de medidas (4m+10).180º e (3m-2).180º ?
R: m possui 4 (quatro) valores distintos.
