Conjuntos numéricos: aprenda a classificação com exercícios

Definimos por conjunto o agrupamento de termos  ou elementos com características parecidas, que são semelhantes em sua natureza. Eles formam “um conjunto”. No estudo e no ensino da Matemática, especificamente, se os elementos semelhantes ou com as mesmas características são os números, então estes  são agrupados em conjuntos denominados  “Conjuntos Numéricos”.

Aprenda agora o básico que você precisa para mandar bem nas questões de Conjuntos Numéricos nas provas do Enem, do Encceja, e dos Vestibulares. Todo ano cai. É fácil, e você vai dominar agora.

O que são conjuntos numéricos

Quando esse conjunto é representado por extenso, escrevemos os números entre chaves { }. Se o conjunto for infinito, irá possuir incontáveis números, então o representamos com reticências.

Conjuntos numéricos fundamentais

Existem cinco conjuntos que são considerados fundamentais, pois são os mais utilizados em problemas e questões matemáticas:

• Naturais;
• Inteiros;
• Racionais;
• Irracionais;
• Reais.

A seguir, vamos começar pelo básico, com os fundamentos para você dominar Conjuntos Numéricos. Acompanhe no resumo do professor Lucas Borguezan, do canal Curso Enem Gratuito.

Conjunto dos Números Naturais

Em algum momento da sua vida, você passou a se interessar por contagens e quantidades. Talvez a primeira ocorrência dessa necessidade tenha sido quando, lá pelos seus três anos de idade, algum coleguinha foi te visitar e começou a mexer nos seus brinquedos.

Provavelmente, mesmo sem saber, naquele momento você começou a utilizar dos números naturais. Afinal, era necessário garantir que nenhum dos seus brinquedos mudasse de proprietário e, mesmo desconhecendo a existência dos números, você já sentia a necessidade de um sistema de numeração.

Em uma situação como essa ,você precisa do mais básico dos conjuntos numéricos: o conjunto dos números naturais. Com a utilização desse conjunto, você pode enumerar brinquedos ou simplesmente registrar a sua quantidade, por exemplo.

O conjunto dos números naturais é representado pela letra ℕ. Abaixo, temos uma representação dos números naturais:

N = {0, 1, 2, 3, 4, 5, 6, 7, …}

N* = {1, 2, 3, 4, 5, 6, 7, …}

N* ⊂ N ∴ N* ∩ N = N*

Ficou difícil de entender? Então vamos decifrar os símbolos que apareceram no exemplo. Os pontos de reticência dão a ideia de infinidade, já que os conjuntos numéricos são infinitos. Utilizamos o símbolo ⊂ para indicar que um conjunto está contido em outro ou que é um subconjunto seu. Já o asterisco indica a ausência do número zero no conjunto.

Por fim, o símbolo ∴ significa “portanto”. Veja na imagem todos os símbolos e o significado deles:

O conjunto numérico do primeiro exemplo inicia-se em zero e é infinito. No entanto, podemos ter a representação de apenas um subconjunto dele que, neste caso, são os mesmos números, só que sem o zero.

A seguir, temos um subconjunto dos números naturais formado pelos quatro primeiro múltiplos de sete:

A = {7, 14, 21, 28}

Conjunto dos Números Inteiros

Mais adiante na sua vida, em uma noite muito fria, você tomou conhecimento da existência de números negativos ao falarem que a temperatura estava em dois graus abaixo de zero. Curioso, você quis saber o que significava isso. Então, notando o seu interesse, alguém resolveu lhe explicar:

Hoje, no final da tarde, já estava bastante frio. A temperatura girava em torno dos 3° C, mas continuou esfriando e ela desceu para 2° C. O frio avançou um pouco mais e a temperatura abaixou para 1° C, e uma hora atrás chegou a 0° C.

Se a temperatura continuava a abaixar e já havia atingido o menor dos números naturais, como, então, representar uma temperatura ainda mais baixa?

Com exceção do zero, cada um dos números naturais possui um simétrico ou oposto. O oposto do 1 é o -1, do 2 o -2 e assim por diante. O sinal “-” indica que se trata de um número negativo, portanto, menor que zero. Os números naturais a partir do 1 são positivos por natureza e o zero é nulo.

O zero e os demais números naturais, juntamente com os seus opostos, formam outro conjunto: o dos números inteiros. Esse conjunto é representado pela letra ℤ. A seguir, temos uma representação dos números inteiros:

Z = {0, ±1, ±2, ±3, ±4, …} onde Z- = {…, -4, -3, -2, -1, 0} e Z+ = {0, 1, 2, 3, 4, …}

Características dos números inteiros

Enquanto os números naturais são infinitos, mas possuem o zero como número inicial, os outros conjuntos numéricos fundamentais não têm, por assim dizer, um ponto de início. No conjunto do exemplo, o zero é um elemento central, pois para cada número à sua direita há um respectivo oposto à sua esquerda.

Como o conjunto dos números naturais é um subconjunto do conjunto dos números inteiros, temos que ℕ ⊂ ℤ. Podemos também dizer que o conjunto dos números inteiros contém (⊃) o conjunto dos números naturais (ℤ ⊃ ℕ).

Com exceção do conjunto dos números naturais, podemos utilizar os caracteres “+” e “-” nos demais conjuntos numéricos fundamentais, como nos exemplos abaixo:

Z+ = {0, 1, 2, 3, 4, 5, 6, 7, …}

Z*+ = {1, 2, 3, 4, 5, 6, 7, …}

Z- = {…, -7, -6, -5, -4, -3, -2, -1, 0}

Z*- = {…, -7, -6, -5, -4, -3, -2, -1}

Note também que ℤ+ = ℕ e que ℤ*+ = ℕ*.

Conjunto dos Números Racionais

Esperto por natureza, você percebeu que havia mais alguma coisa além disso. Você viu no termômetro que entre um número e outro existiam várias marcações. Qual a razão disso?

Foi-lhe explicado, então, que a temperatura não muda abruptamente de 20° C para 21° C, ou de -3° C para -4° C.Em vez disso, as marcações são de décimos em décimos. Para passar de 20° C para 21° C, por exemplo, primeiro a temperatura sobe para 20,1° C, depois para 20,2° C e continua assim até chegar em 21° C. Esses são números pertencentes ao conjunto dos números racionais.

Números racionais são todos aqueles que podem ser expressos na forma de fração. O numerador e o denominador da fração devem pertencer ao conjunto dos números inteiros e, obviamente, o denominador não poderá ser igual a zero, pois não há divisão por zero.

O número 20,1, por exemplo, pode ser expresso como 201/100, assim como 0,375 pode ser expresso como 3/8, e 0,2 pode ser representado por 1/5.

Note que, se dividirmos quatro por nove, iremos obter 0,444…, que é um número com infinitas casas decimais, todas elas iguais. Apesar disso, ainda é um número racional, pois pode ser expresso como 4/9.

O conjunto dos números racionais é representado pela letra ℚ. Ele é um subconjunto dos números racionais. Portanto, temos que ℤ ⊂ ℚ. Afinal, todos os números inteiros podem ser escritos em forma de fração.

Abaixo, temos um exemplo de conjunto numérico com três elementos que é subconjunto dos números racionais:

{-5, 1/9, 1}

Conjunto dos Números Irracionais

Depois, mais curioso ainda, você perguntou: “Se os números racionais são todos aqueles que podem ser expressos na forma de fração, então existem aqueles que não podem ser expressos dessa forma?”

Exatamente! Os números que não podem ser expressos em forma de fração são os irracionais. Provavelmente, os mais conhecidos são o Pi (π), o número de Euler (e) e a raiz quadrada de dois (√2). Se você se dispuser a calcular tal raiz, passará o restante de sua existência e jamais conseguirá fazê-lo.

O motivo é que o resultado de √2 tem infinitas casas decimais e, diferentemente das dízimas, elas não são periódicas e não podem ser expressas na forma de fração. Essa é uma das características dos números irracionais.

A raiz quadrada dos números naturais é uma ótima fonte de números irracionais. De fato, a raiz quadrada de qualquer número natural que não seja um quadrado perfeito é um número irracional.

√120, por exemplo, é um número irracional, pois 120 não é um quadrado perfeito. Em outras palavras, não há um número natural que multiplicado por ele mesmo resulte em 120. Já √121 é um número natural, pois 11² = 121.

A letra I representa o conjunto dos números irracionais.

Veja um exemplo de de subconjunto dos números irracionais:

{π, e, √2, √3}

Diferentemente do que acontece com os números racionais, a realização de qualquer uma das quatro operações aritméticas entre dois números irracionais quaisquer não terá, obrigatoriamente, também um número irracional como resultado. O resultado poderá tanto pertencer a I quanto pertencer a ℚ.

Antes de ir para a parte final da aula, relembre neste resumo os conjuntos numéricos que vimos até agora :

Conjunto dos Números Reais

Anteriormente, vimos que um número natural também é um número inteiro (ℕ ⊂ ℤ), assim como um número inteiro também é um número racional (ℤ ⊂ ℚ). Portanto, ℕ ⊂ ℤ ⊂ ℚ. Vimos também que os números racionais não estão contidos no conjunto dos números irracionais e vice-versa. A intersecção desses conjuntos resulta no conjunto vazio ℚ ∩ I = ∅.

A intersecção (∩) é uma operação por meio da qual obtemos um conjunto de todos os elementos que pertencem simultaneamente a todos os conjuntos envolvidos. Sejam dois conjuntos A = {1, 2, 3, 4} e B = {5, 4, 3}, a intersecção entre esses dois conjuntos será A ∩ B = {3, 4}.

O conjunto dos números reais é representado pela letra ℝ e é formado pela união dos conjuntos dos números racionais com os irracionais, simbolicamente representados por ℝ = ℚ ∪ I.

A união (∪) é uma operação por meio da qual obtemos um conjunto de todos os elementos que pertencem ao menos a um dos conjuntos envolvidos. Por exemplo: sejam dois conjuntos A = {1, 2, 3, 4} e B = {5, 4, 3}, a união desses dois conjuntos será A ∪ B = {1, 2, 3, 4, 5}.

O conjunto dos números racionais está contido no conjunto dos números reais ℚ ⊂ ℝ assim como o conjunto dos números irracionais é subconjunto do conjunto dos números reais (I ⊂ ℝ).

Por meio dos caracteres especiais + e *, por exemplo, podemos representar o conjunto dos números reais positivos por ℝ*+.

Abaixo temos um exemplo de conjunto numérico contendo números reais:

{√7, -3, 4/7, 8}

Se quiser aprender mais sobre os números reais é só conferir nossa aula sobre operações com intervalos reais!

Diagrama dos conjuntos numéricos fundamentais

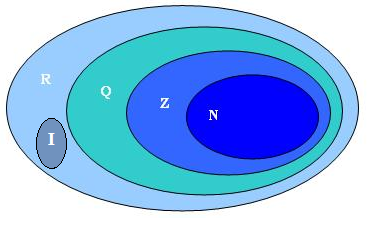
Por meio do diagrama dos conjuntos numéricos, podemos facilmente observar que o conjunto dos números reais (ℝ) é resultado da união do conjunto dos números racionais com o conjunto dos números irracionais (ℝ = ℚ ∪ I).

Observamos também que o conjunto dos números inteiros está contido no conjunto dos números racionais (ℤ ⊂ ℚ) e que os números naturais são um subconjunto dos números inteiros (ℕ ⊂ ℤ).

Como podemos ver, os diagramas nos ajudam a trabalhar mais facilmente com conjuntos. Ainda neste diagrama, rapidamente identificamos que os números naturais são também números reais (ℕ ⊂ ℝ), mas não são números irracionais (ℕ ⊄ I).

Isso porque o conjunto dos números irracionais não contém o conjunto dos números naturais (I ⊅ ℕ). Ao contrário, é o conjunto dos números racionais que os contêm (ℚ ⊃ ℕ), assim como o conjunto dos números reais (ℝ ⊃ ℕ) e dos inteiros (ℤ ⊃ ℕ).

O próximo passo nos seus estudos sobre o assunto é resolver os exercícios e ver a aula sobre operações com conjuntos numéricos. Bons estudos!

União e Intersecção de Conjuntos Numéricos

Veja agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, exemplos de questões resolvidas. Assim você aprende mais rápido como gabaritar nas provas nos problemas de Conjuntos Numéricos:

Exercícios de conjuntos numéricos

Para finalizar seus estudos, veja como os conjuntos numéricos aparecem no Enem e nos vestibulares:

1- (ENEM/2016)    

Nas construções prediais são utilizados tubos de diferentes medidas para a instalação da rede de água. Essas medidas são conhecidas pelo seu diâmetro, muitas vezes medido em polegada. Alguns desses tubos, com medidas em polegada, são os tubos de 1/2, 3/8 e 5/4.

Colocando os valores dessas medidas em ordem crescente, encontramos

a) 1/2, 3/8, 5/4.

b) 1/2, 5/4, 3/8.

c) 3/8, 1/2, 5/4

d) 3/8, 5,4, 1/2

e) 5/4, ½, 3/8

2 – (IFAL/2019)    

Considere o conjunto A = {1,2,3,4,5} e o conjunto B = {3,4,5,6,7}. O conjunto que representa A ∩ B será dado por:

a) {1,2,3}

b) {1,2,3,4,5}

c) {3,4,5}

d) {1,2,6,7}

e) {1,2,3,4,5,6,7}

3 – (UNIC MT/2018)    

Admitindo-se que U, V e W são conjuntos não vazios, tais que existe, pelo menos, um U que é V e que todo V é W, pode-se concluir necessariamente que

01. todo W é V.

02. todo W é U.

03. todo U é W.

04. algum U é W.

05. nada que não seja W é U.

4 – (ENEM/2004)    

Um fabricante de cosméticos decide produzir três diferentes catálogos de seus produtos, visando a públicos distintos. Como alguns produtos estarão presentes em mais de um catálogo e ocupam uma página inteira, ele resolve fazer uma contagem para diminuir os gastos com originais de impressão. Os catálogos C₁, C₂ e C₃ terão, respectivamente, 50, 45 e 40 páginas.

Comparando os projetos de cada catálogo, ele verifica que C₁ e C₂ terão 10 páginas em comum; C₁ e C₃ terão 6 páginas em comum; C₂ e C₃ terão 5 páginas em comum, das quais 4 também estarão em C₁.

Efetuando os cálculos correspondentes, o fabricante concluiu que, para a montagem dos três catálogos, necessitará de um total de originais de impressão igual a:

a) 135.

b) 126.

c) 118.

d) 114.

e) 110.

GABARITO: 

1. C
2. C
3. 04
4. C