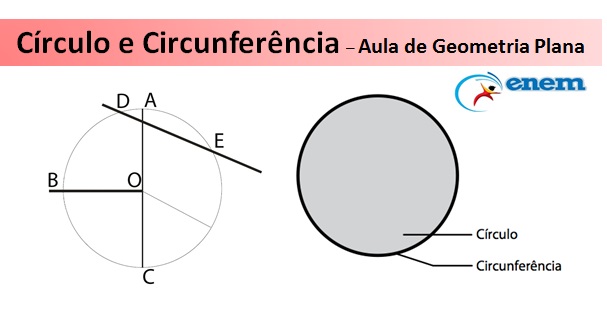
Você sabe a diferença entre um círculo e uma circunferência? Nesta aula de Geometria Plana você pode revisar tudo sobre essas duas formas geométricas para as questões de Matemática no Enem e no Vestibular. E tem lista de exercícios! Confira abaixo.
Revisão de Geometria Plana. Veja sobre Círculo e Circunferência. Sim, têm diferenças importantes. Veja nesta aula preparatória para o Enem e o Vestibular. E veja a lista de exercícios depois da vídeo-aula. Vamos começar pelas Definições:
Circunferência é o lugar geométrico dos pontos de um plano, equidistantes de um ponto fixo chamado centro. Então, nada de confundir Círculo e Circuferência.
Leia novamente a definição acima de Circunferência antes de observar a imagem abaixo, e de ler a seguir o que é um Círculo.
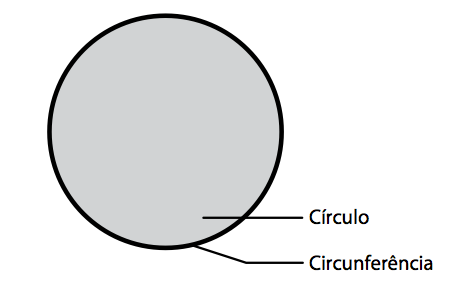Círculo é a superfície plana limitada por uma circunferência ou a reunião de uma circunferência e seu interior.
Diferenças entre Círculo e Circunferência
Aprenda em cinco minutos quais são os elementos principais para lidar com Círculo e Circunferência, antes de resolver os Exercícios que estão logo abaixo. Veja agora esta revisão do Professor Lucas Borguezan, do canal do Curso Enem Gratuito.
Valeu pra você? Aprendeu as diferenças entre um Círculo e uma Circunferência? Se precisar,veja o resumo novamente antes de prosseguir.
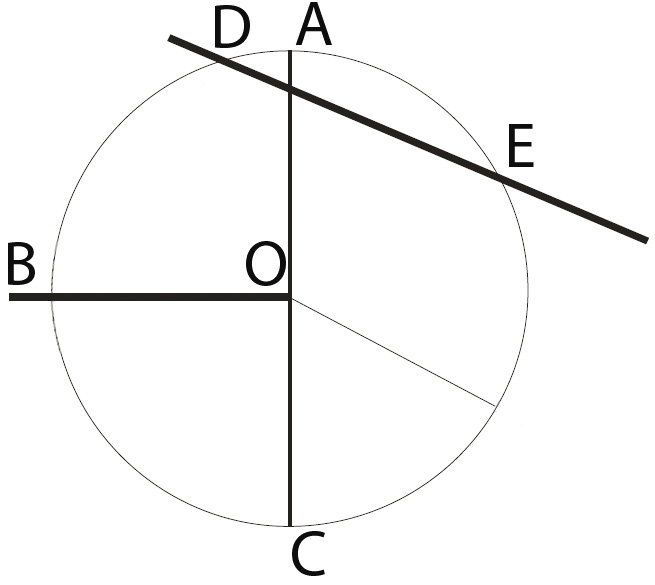
Elementos Principais do Círculo e da Circunferência:
- O = centro da circunferência
- Segmento AO = raio da circunferência (r)
- Segmento AC = diâmetro da circunferência = dobro do raio
- Linha DE = corda
- Perímetro (comprimento da circunferência)
- C = 2.π.r (Dois ‘pi’ erre)
- Área do círculo
- A = π.r2 (‘pi’ erre ao quadrado)
No estudo analítico da circunferência, os elementos raio, diâmetro e centro da circunferência são fundamentais para conclusões de diversos problemas. Posteriormente, será apresentada a definição de círculo e suas características geométricas.
A circunferência possui características não comumente encontradas em outras figuras planas, como o fato de ser a única figura plana que pode ser rodada em torno de um ponto sem modificar sua posição aparente.
É também a única figura que é simétrica em relação a um número infinito de eixos de simetria.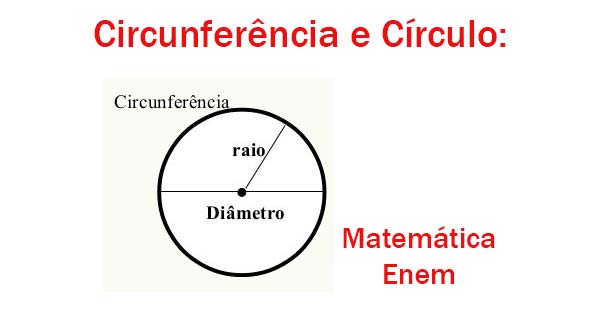
A circunferência é importante em praticamente todas as áreas do conhecimento como nas Engenharias, Matemática, Física, Química, Biologia, Arquitetura, Astronomia, Artes e também é muito utilizado na indústria e bastante utilizada nas residências das pessoas.
Definimos circunferência como uma linha curva fechada que possui um ponto central, que, por sua vez, é chamado de origem (O) e é equidistante, ou seja, apresenta a mesma distância em todos os pontos da linha curva em relação ao centro.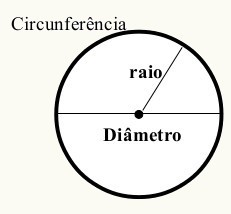 
Toda circunferência possui raio e diâmetro. Veja novamente na imagem acima para gravar bem.
O Comprimento da circunferência
Quanto maior for o raio (ou o diâmetro) de uma circunferência maior será o seu comprimento. Imagine que você vai caminhar em torno de uma praça circular: você andará menos em uma praça com 500 metros de diâmetro do que numa praça com 800 metros de diâmetro.
No exemplo abaixo, cada uma das três circunferências foi cortada no ponto marcado com uma tesourinha, e a linha do traçado de cada uma delas foi esticada.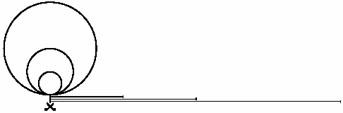
Círculo
Círculo (ou disco) é o conjunto de todos os pontos de um plano cuja distância a um ponto fixo 0 é menor ou igual que uma distância r dada. Quando a distância é nula, o círculo se reduz a um ponto.
O círculo é a reunião da circunferência com o conjunto de pontos localizados dentro da mesma. É uma figura geométrica bastante comum em nosso dia-a-dia. Observe à sua volta quantos objetos circulares estão presentes: nas moedas, nos discos, a mesa de refeição…
Agora pense, o que faríamos para:
* riscar no tecido o contorno de uma toalha de mesa redonda?
* desenhar um círculo no seu caderno?
* marcar o limite das escavações de um poço no chão?
Quando falamos em círculo, ninguém tem dúvida quanto ao formato dessa figura geométrica. No entanto, em geometria, costuma-se fazer uma pequena distinção entre círculo e circunferência, sobre a qual você já deve ter ouvido falar.
A superfície de uma moeda, de uma pizza ou de um disco é um círculo.
Quando riscamos no papel ou no chão apenas o contorno do círculo, este contorno é chamado circunferência.
Propriedades básicas do círculo e da circunferência cabeçalho 2)
O ponto C, centro da circunferência, não pertence a ela, mas pertence ao círculo. Dessa maneira, dado um ponto A qualquer (lembrando que dAC é a distância entre A e C), as posições relativas entre A e uma circunferência são:
1 – A é ponto da circunferência, se dAC = r;
2 – A é ponto externo à circunferência, se dAC > r;
3 – A é ponto interno à circunferência, se dAC < r; As posições relativas entre A e o círculo são: 1 – A é ponto do círculo, se dAC ≤ r 2 – A é ponto externo ao círculo, se dAC > r
Para não esquecer o Círculo: – Círculo (ou disco) é o conjunto de todos os pontos de um plano cuja distância a um ponto fixo 0 é menor ou igual que uma distância ‘r’ dada.
Os ângulos na Circunferência
Confira com o professor Lucas uma introdução aos ângulos da Circunferência
Veja o que mais cai de Matemática no Enem
Marque nos favoritos os Temas que você precisa revisar e veja as dicas de Matemática e todas as matérias: Tem aula hoje e amanhã também.
- 10 Temas que mais caem no Enem – Plano de Estudos
- Plano de Estudos de Química Enem
- Plano de Estudos de Biologia Enem
- Plano de Estudos de Matemática Enem
- Simulado Enem Gratuito – Provas de todas as matérias
- Plano de Estudos Enem Completo – Todas as matérias
Desafios sobre Círculo e Circunferência
Questão 01
Determinar o diâmetro e a área de um círculo (respectivamente), cujo perímetro mede 36π cm.
a) 63 cm e 300 π cm2
b) 36 cm e 324 π cm2
c) 50 cm e 324 π cm2
d) 36 cm e 300 π cm2
e) 43 cm e 324 π cm2
Dica 1 – Estude sobre Circunferência em mais esta aula de revisão para Matemática Enem. O Exame Nacional do Ensino Médio está chegando, estude com a gente! – https://blogdoenem.com.br/circunferencia-matematica-enem/
Questão 02
A roda de um automóvel tem um diâmetro que mede 50 cm. Determine a distância percorrida por esse veículo após uma de suas rodas completar 1750 voltas. Adotar π = 3,14 e supor que a roda não deslize durante a rolagem.
a) 2,82 km
b) 3 km
c) 3,6 km
d) 2,75 km
e) 2,91 km
Dica 2 – Preparado para o Exame Nacional do Ensino Médio? Revise tudo sobre Geometria Analítica em mais uma aula de Matemática Enem que preparamos para você – https://blogdoenem.com.br/geometria-analitica-matematica-enem/
Questão 03
Testes efetuados em um pneu de corrida constataram que, a partir de 185 600 voltas, ele passa a se deteriorar, podendo causar riscos à segurança do piloto. Sabendo que o diâmetro do pneu é de 0,5 m, ele poderá percorrer, sem riscos para o piloto, aproximadamente:
a) 93 km
b) 196 km
c) 366 km
d) 592 km
e) 291 km
Dica 3 – Revise sobre as Funções Trigonométricas em mais esta aula preparatória para prova de Matemática Enem. Estude conosco para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/funcoes-trigonometricas-matematica-enem/
Questão 04
O ponteiro dos minutos de um relógio mede 4 cm. Supondo π = 3, a distância, em centímetros, que a extremidade desse ponteiro percorre em 25 minutos é:
a) 15
b) 12
c) 20
d) 25
e) 10
Questão 05
Em um motor há duas polias ligadas por uma correia, de acordo com o esquema abaixo.
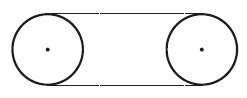
Se cada polia tem raio de 10 cm e a distância entre seus centros é de 30 cm, qual das medidas abaixo mais se aproxima do comprimento da correia?
a) 122,8 cm
b) 102,4 cm
c) 92,8 cm
d) 50 cm
e) 32,4 cm
Questão 06
Os raios das rodas traseiras de um trator medem 75 cm e dão 30 voltas, ao mesmo tempo em que as rodas dianteiras dão 90 voltas. O raio de cada uma das rodas dianteiras é:
a) 20 cm
b) 30 cm
c) 25 cm
d) 15 cm
e) 22 cm.
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
