Triângulos e quadrados caem direto. Formas geométricas são os formatos dos objetos que observamos. Eles podem ser planos, como quadrados e triângulos, ou espaciais, como uma esfera ou uma pirâmide.
A geometria, área da Matemática que estuda as formas geométricas, desenvolveu uma série de classificações para conseguirmos estudar os diferentes formatos.
Nesta aula você vai saber mais sobre algumas dessas classificações, como os polígonos, os poliedros e os fractais. O primeiro passo é você ver o resumo básico do professor Lucas Borguezan, do canal do Curso Enem Gratuito, para você aprender os cálculos de área e de perímetro do quadrado e do retângulo.
Formas geométricas planas
As formas geométricas planas, ou figuras planas, são aquelas que possuem apenas duas dimensões: comprimento e largura. Alguns exemplos são círculo, quadrado, triângulo, retângulo, trapézio, hexágono, pentágono, paralelogramo e losango. Dentro das figuras planas, existe a classificação entre polígonos e não polígonos.
Polígonos
Os polígonos são as formas geométricas planas que são fechadas por segmentos de reta. Em um polígono, os segmentos de reta não podem se cruzar. Cada segmento de reta forma um lado do polígono.
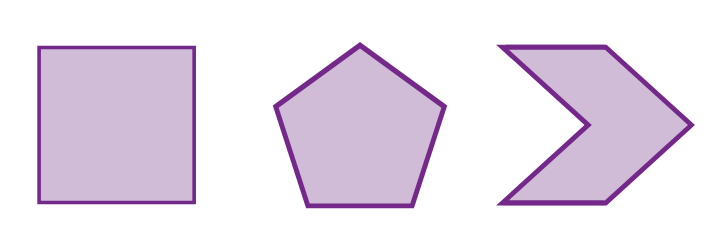Exemplos de polígonos
Veja as Formas Geométricas que mais caem no Enem
Confira no resumo com o professor Lucas Borguezan
Os nomes dos polígonos são dados de acordo com o seu número de lados. Por exemplo:
- Triângulo: 3 lados
- Quadrilátero: 4 lados
- Pentágono: 5 lados
- Hexágono: 6 lados
- Heptágono: 7 lados
- Octógono: 8 lados
- Eneágono: 9 lados
- Decágono: 10 lados
- Dodecágono: 12 lados
- Icoságono: 20 lados
Alguns polígonos, como o triângulo, quadriláteros, pentágonos e hexágonos, são amplamente estudados na matemática. Por isso, existem fórmulas para cálculos de área e perímetro e outras propriedades. Além disso, costumam ser bastante cobrados no Enem e nos vestibulares. Aqui no site você pode conferir aulas sobre os triângulos e sobre os quadriláteros.
Círculo não é um polígono
Nem todas as formas geométricas planas são polígonos. Se uma figura plana tiver curvas, se os segmentos interceptam-se ou então se a figura não for fechada, ela não será um polígono.
Essas formas geométricas são chamadas de não polígonos. O círculo, por exemplo, é um não polígono comum em nosso dia-a-dia.
Exemplos de não polígonos
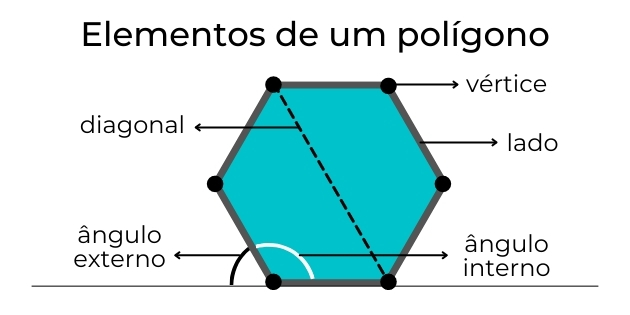
Elementos de um polígono
Existem 5 elementos principais em um polígono: vértices, lados, diagonais, ângulos internos e ângulos externos. O vértice é como se fosse o “canto” ou “esquina” do polígono. Ao ligar dois vértices consecutivos através de uma reta, obtemos um lado.
Enquanto isso, se você fizer a junção de dois vértices que não são consecutivos, você irá obter uma diagonal. Também é possível formar ângulos na parte de dentro do polígono ou figura plana. Esses são chamados de ângulos internos. Se prolongarmos o ângulo para a parte de fora do polígono, ele passa a ser o ângulo externo.
É possível que você encontre questões no Enem ou nos vestibulares que exijam que você saiba calcular o número de lados ou de diagonais de uma forma geométrica plana, mas sem te dizer qual é. Para que você consiga resolver esse tipo de problema existe uma fórmula simples:
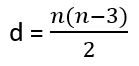
Onde:
- d = número de lados do polígono
- n = número de diagonais do polígono
Resumo sobre polígonos
Para saber mais sobre a classificação e os elementos dos polígonos, veja a videoaula do prof. Sarkis no canal do Curso Enem Gratuito:
Formas geométricas espaciais
As formas geométricas espaciais são as formas que possuem três dimensões: comprimento, altura e largura. Elas também são conhecidas como sólidos geométricos. Alguns exemplos são a pirâmide, o cubo, a esfera, o cone e o cilindro. Os sólidos geométricos podem ser classificados em poliedros e não poliedros.
Poliedros
Os sólidos geométricos são chamados de poliedros quando possuem apenas polígonos em sua superfície.
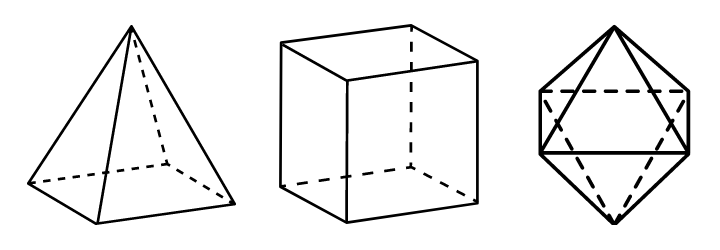A pirâmide, o cubo e o octaedro são exemplos de poliedros
Assim como os polígonos, os nomes dos poliedros são dados de acordo com o seu número de faces. Por exemplo:
- Tetraedro: 4 faces
- Pentaedro: 5 faces
- Hexaedro: 6 faces
- Heptaedro: 7 faces
- Octaedro: 8 faces
- Decaedro: 10 faces
- Dodecaedro: 12 faces
- Icosaedro: 20 faces
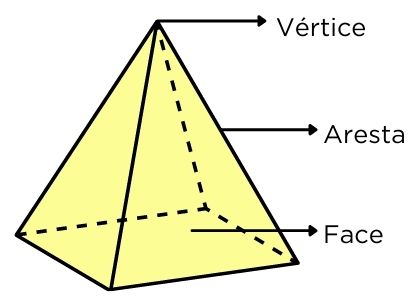
Cada polígono compõe uma face do poliedro. Enquanto isso, a reta de interseção entre duas faces é chamada de aresta. Por fim, o ponto de interseção de várias arestas chama-se vértice.
Não poliedros
Os não poliedros, também chamados de corpos redondos, são os sólidos espaciais que apresentam superfícies arredondadas. Essas figuras geométricas também recebem o nome de corpos redondos ou sólidos de revolução.
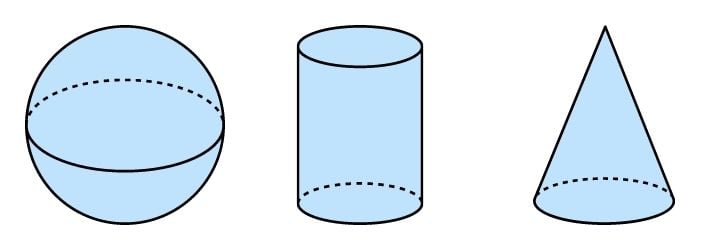A esfera, o cilindro e o cone são exemplos de não poliedros.
Saiba mais sobre os sólidos de revolução com a aula do canal do Curso Enem Gratuito:
Relação de Euler
A relação de Euler é uma equação que podemos determinar a quantidade de vértices, arestas e faces de um poliedro convexo e alguns não convexos. Veja:
V + F = A + 2
Onde:
- V = número de vértices
- F = número de faces
- A = número de arestas
Em seguida, vamos resolver um exercício para que você entenda como utilizar a Relação de Euler.
(FAAP – SP) Em um poliedro convexo, o número de arestas excede o número de vértices em 6 unidades. Qual o número de faces?
Solução: Seja V = quantidade de vértices do poliedro, como a quantidade de arestas excede o número de vértices em 6 unidades, a quantidade de arestas é expressa pela equação A = V + 6. Substituindo essas igualdades na relação de Euler obtemos:
V – (V + 6)+F= 2
Aplicando a distributiva temos a seguinte igualdade:
V – V – 6 + F= 2
F = 2+6
F = 8
Portanto, o poliedro possui 8 faces.
Resumo sobre poliedros
Veja mais exemplos de cálculos envolvendo poliedros com esta videoaula:
Fractais
O último tipo de forma geométrica que vamos ver nesta aula são os fractais. A palavra fractal vem do latim fractus, que significa irregular ou quebrado. Os fractais são formas geométricas em que cada parte da figura se assemelha ao todo. Existe um padrão em toda a figura que é repetido em cada uma de suas partes.
Os fractais são estudados por duas áreas da física e da matemática que se chamam Sistemas Dinâmicos e Teoria do Caos. As equações que envolvem essas formas descrevem porque certos fenômenos, como o fluxo dos rios, por exemplo, parecerem aleatórios, mas obedecem a certas regras.
O brócolis romanesco é um exemplo da natureza que é formado por fractais.
Exercícios sobre formas geométricas
Por fim, resolva os exercícios e saiba como este conteúdo é cobrado no Enem e em vestibulares.
1 – (UEG GO/2020)
O poliedro convexo regular cujo número de arestas é o dobro do número de vértices é o octaedro. O número de vértices do octaedro é
a) 4
b) 20
c) 12
d) 8
e) 6
2- (ENEM/2017)
O hábito cristalino é um termo utilizado por mineralogistas para descrever a aparência típica de um cristal em termos de tamanho e forma. A granada é um mineral cujo hábito cristalino é um poliedro com 30 arestas e 20 vértices. Um mineralogista construiu um modelo ilustrativo de um cristal de granada pela junção dos polígonos correspondentes às faces.
Supondo que o poliedro ilustrativo de um cristal de granada é convexo, então a quantidade de faces utilizadas na montagem do modelo ilustrativo desse cristal é igual a
a) 10.
b) 12.
c) 25.
d) 42.
e) 50.
3- (UECE/2014)
Se, em um polígono convexo, o número de lados n é um terço do número de diagonais, então o valor de n é
a) 9.
b) 11.
c) 13.
d) 15.
Gabarito:
- E
- B
- A
