Prepare-se para as provas do Exame Nacional do Ensino Médio com esta aula completa sobre a resolução dos Polinômios. Veja como fazer a Soma, Subtração, Divisão e Multiplicação das equações polinomiais para mandar bem nas provas. Vem, que é pura matemática Enem.
Definições e operações polinomiais: polinômio é uma expressão algébrica composta por dois ou mais monômios.
O nome pode parecer estranho para a maioria das pessoas. E, logo vem na cabeça a impressão de que são contas difíceis de fazer. Mas, na verdade, é tudo bem simples.
Comece a sua revisão por este resumo rápido com o professor Lucas Borguezan, do canal do Curso Enem Gratuito. Você aprende de uma vez por todas, e gabarita nas questões do Enem, do Encceja, e do vestibular. COnfira:
Os Polinômios – Podemos definir como equação polinomial toda equação escrita na forma:![]()
O Grau de um polinômio
O grau de um termo de uma variável em um polinômio é o expoente dessa variável nesse termo. Por exemplo, em 2x³ + 4x² + x + 7, o termo de maior grau é 2x³; esse termo, e, portanto, todo o polinômio, é dito ser de grau 3.
Os Polinômios Idênticos
São polinômios de mesmo grau, que possuem os coeficientes correspondentes iguais.
Operações com Polinômios
Adição e Subtração
Considere os polinômios –2x² + 5x – 2 e –3x³ + 2x – 1. Vamos efetuar a adição e a subtração entre eles.
Veja como fazer a Adição
- (–2x² + 5x – 2) + (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
- –2x² + 5x – 2 – 3x³ + 2x – 1 → reduzir os termos semelhantes
- –2x² + 7x – 3x³ – 3 → ordenar de forma decrescente de acordo com a potência
- –3x³ – 2x² + 7x – 3
Veja como fazer a Subtração
- (–2x² + 5x – 2) – (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
- –2x² + 5x – 2 + 3x³ – 2x + 1 → reduzir os termos semelhantes
- –2x² + 3x – 1 + 3x³ → ordenar de forma decrescente de acordo com a potência
- 3x³ – 2x² + 3x – 1
Aula Gratuita: As Quatro Operações com Polinômios
Veja um resumo simples e rápido com o professor Sérgio Sarkis, do Curso Enem Gratuito, para você aprender a resolver Polinômios:
Muito bom este resumo! Agora, veja a demonstração de Multiplicação e Divisão de Polinômios:
Multiplicação de polinômio por polinômio
- Para efetuarmos a multiplicação de polinômio por polinômio, devemos utilizar a propriedade distributiva. Veja o exemplo:
- (x – 1) . (x2 + 2x – 6)
- x.x2 + x.2x – x.6 + (-1).x2 + (-1).2x – (-1).6
- x³ +2x² – 6x – x² – 2x + 6
 reduzindo os termos semelhantes.
reduzindo os termos semelhantes. - x³ + x² – 8x + 6
Divisão de polinômios![]()
Vamos dividir um polinômio por um monômio, com o intuito de entendermos o processo operatório. Observe:
Veja a videoaula do Curso Enem Gratuito sobre a divisão de polinômios:
Dica 1 – Tire todas as suas dúvidas sobre Funções Polinomiais de 2o grau em mais esta aula de revisão para a prova de Matemática Enem que preparamos para você – https://blogdoenem.com.br/funcao-polinomial-2o-grau-revisao-matematica-enem/
Exercício Resolvido
(G1 – utfpr 2011) Quais são os polinômios que representam o quociente q(x) e o resto r(x) da divisão do polinômio
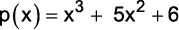 pelo polinômio
pelo polinômio 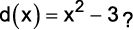
a) q(x) = – (x + 5) e r(x) = 3x + 21.
b) q(x) = x + 5 e r(x) = – (3x + 21).
c) q(x) = x – 5 e r(x) = – 3x + 21.
d) q(x) = – (x + 5) e r(x) = 3x – 21.
e) q(x) = x + 5 e r(x) = 3x + 21.
Resposta da questão: [E]
Efetuando a divisão, temos:
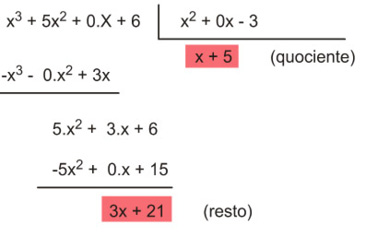
Função Polinomial
Podemos definir como função polinomial as funções escritas na forma:
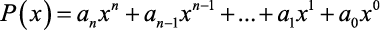
Saiba mais sobre os Polinômios nesta aula do canal Aulalivre.net, disponível no Youtube. Após assistir, revise o que você aprendeu respondendo aos nossos desafios!
[youtube http://www.youtube.com/watch?v=XySESQb3TWE]
Desafios
Questão 1
(Upe 2011) Para que o polinômio 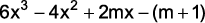 seja divisível por x – 3, o valor da raiz quadrada do módulo de m deve ser igual a
seja divisível por x – 3, o valor da raiz quadrada do módulo de m deve ser igual a
a) 0
b) 1
c) 2
d) 3
e) 5
Dica 2 – O dia das provas está chegando, que tal revisar algumas aulas importantes. Revise tudo sobre Função Polinomial do 1º grau nesta aula de Matemática Enem – https://blogdoenem.com.br/funcao-polinomial-do-1o-grau-matematica-enem/
Questão 2
2. (G1 – ifsc 2011) Dada a função polinominal 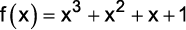 ,
,
o valor de
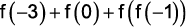 é:
é:
a) – 20.
b) -18.
c) – 16.
d) 20.
e) 16.
Dica 3 – Acompanhe esta revisão sobre Equações Polinomiais do 1º e 2º grau e fique preparado para a prova de Matemática Enem – https://blogdoenem.com.br/equacoes-polinomiais-1o-e-2o-grau-matematica-enem/
Questão 3
(Ufjf 2011) Dados dois polinômios 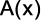 e
e 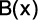 , sabe-se que
, sabe-se que 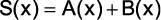
é um polinômio de grau 8 e que
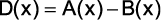
é um polinômio de grau 5 . É correto afirmar:
a) O polinômio 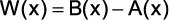 tem grau 8.
tem grau 8.
b) Os polinômios 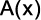 e
e 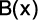 têm o mesmo grau.
têm o mesmo grau.
c) O polinômio 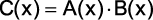 tem grau 13.
tem grau 13.
d) O polinômio 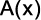 tem grau 5.
tem grau 5.
e) O grau do polinômio 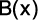 é menor que 7.
é menor que 7.
Questão 4
(Ufsm 2008) Para embalar pastéis folheados, são utilizadas folhas retangulares de papel celofane cujas dimensões são as raízes reais positivas do polinômio P(x) = x3 – 12x2 + 20x + 96. Sabendo que uma das raízes é – 2, o produto de duas raízes poderá ser
a) 12
b) 16
c) 96
d) – 48
e) – 16
Questão 5
(Ufg 2007) Considere o polinômio:
p(x) = (x – 1)(x – 3)2(x – 5)3(x – 7)4(x – 9)5(x – 11)6.
O grau de p(x) é igual a
a) 6
b) 21
c) 36
d) 720
e) 1080
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!

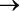 reduzindo os termos semelhantes.
reduzindo os termos semelhantes.