Nesta aula de Conhecimentos Geométricos você irá revisar sobre o Teorema de Tales. É incrivelmente simples e inteligente ao mesmo tempo. Uma fórmula genial de cálculo de Proporções na Geometria. Conteúdo sempre importante na prova de Matemática Enem
O Teorema de Tales – Cálculos geométricos envolvendo ‘Proporção’. É incrível a lógica envolvida. É simples e dá resultados extraordinários. Veja!
O Teorema de Tales é uma importante ferramenta utilizada há muitos e muitos séculos na determinação de medidas utilizando a proporcionalidade. Reza a lenda que a construção das antigas Pirâmides no Egito, por exemplo, só foi possível a partir dos cálculos derivados do Teorema de Tales.
A origem do Teorema está com o filósofo e matemático grego Tales de Mileto, que viveu entre 623 a.C e 548 a.C. Para compreender a dimensão destas proposições, leia a frase seguinte com muita calma, e articulando o seu pensamento com a imagem associada:
“Se duas ou mais retas paralelas forem cortadas por um feixe retas transversais, formam-se nas transversais segmentos correspondentes proporcionais“. É a essência para compreender o Teorema de Tales.
Observe agora a figura, e vá aplicando o raciocínio da proposição. Leia novamente o parágrafo acima e volte a esta imagem para reconstruir seu raciocínio de acordo com a definição: 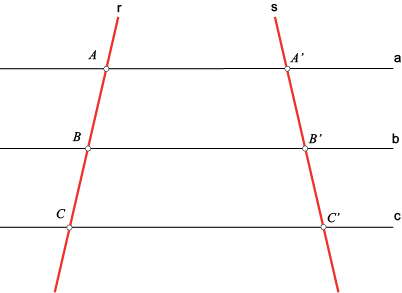
As características que dão o fundamento para o Teorema de Tales estão presentes na figura acima, e podem ser verificadas também nos seguintes aspectos:
- As retas a, b e c são paralelas
- As retas r e s são as transversais ( retas que cortam as paralelas )
- Os segmentos AB e A’B’ são correspondentes assim como os segmentos BC e B’C’
De acordo com Tales podemos construir a seguinte proporção:
A B A’ B’ = B C B’ C’ = A C A’ C’
Dica do Blog: Aula grátis com resumo completo:
Veja com o professor Sérgio Sarkis, do canal Curso Enem Gratuito, um resumo rápido com exercício resolvido para você dominar os fundamentos que estão presentes no Teorema de Tales.
Muito bom este resumo do professor Sarkis!
Dica 1 – Preparado para enfrentar a prova de Matemática Enem? Revise os conceitos relacionados aos ângulos e suas classificações para gabaritar na prova – https://blogdoenem.com.br/angulos-matematica-geometria-enem/
Aula Gratuita sobre o Teorema de Tales
Saiba mais sobre o Teorema de Tales com esta aula do canal Me Salva:
Desafios sobre o Teorema de Tales:
Considerando o Teorema de Tales, nas figuras, a // b // c, calcule o valor de x:
Questão 1
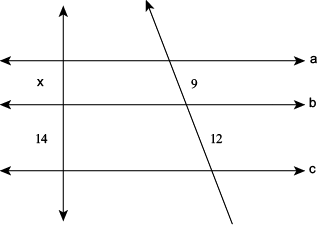
a) 10
b) 10,5
c) 11
d) 12,5
e) 13
Questão 2
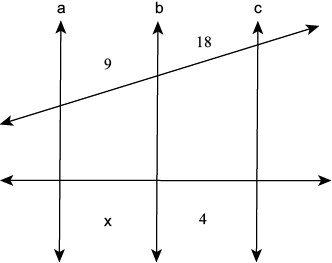
a) 1
b) 1,5
c) 1,8
d) 2
e) 2,5
Questão 3
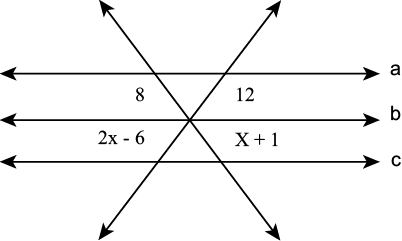
a) 10
b) 12
c) 13
d) 14
e) 15
Dica 2 – Estude para a prova de Matemática Enem com esta aula sobre Razões e proporcionalidade – https://blogdoenem.com.br/razoes-proporcoes-matematica-enem/
Questão 4
A figura abaixo nos mostra duas avenidas que partem de um mesmo ponto A e cortam duas ruas paralelas. Na primeira avenida, os quarteirões determinados pelas ruas paralelas tem 80 m e 90 m de comprimento, respectivamente. Na segunda avenida, um dos quarteirões determinados mede 60 m. Qual o comprimento do outro quarteirão ?
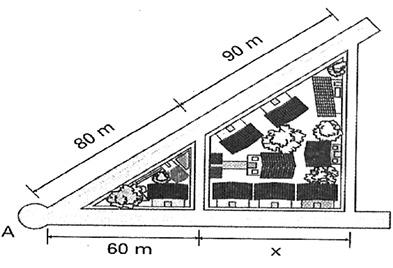
a) 67,5
b) 69
c) 70,5
d) 72
e) 75
Dica 3 – Fique preparado para a prova de Matemática do Enem revisando o conteúdo com esta aula completa sobre intervalos em R – https://blogdoenem.com.br/intervalos-r-matematica-enem/
Questão 5
Na figura abaixo, um garoto está em cima de um banco. Qual é a altura desse garoto que projeta uma sombra de 1,2 m, sabendo que o banco de 30 cm projeta uma sombra de 40 cm ?

a) 75 cm
b) 80 cm
c) 0,9 m
d) 1,10 m
e) 1,2 m
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!

