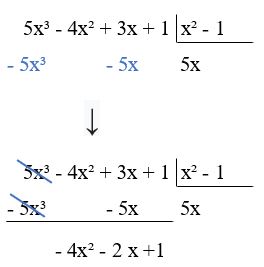Adição, subtração, multiplicação e divisão de polinômios

Devemos estudar os polinômios em razão de sua importância dentro da matemática e demais áreas. Assim, é preciso saber esse conteúdo para entender equações de primeiro grau, segundo grau e exercícios de geometria, por exemplo.

Por isso, nesta aula você vai aprender o que é polinômio, como identificar seu grau, e como realizar operações envolvendo adição, subtração, multiplicação e divisão de polinômios!

Uma função polinomial ou simplesmente polinômio, é toda função definida pela relação P(x)=anxn + an-1.xn-1 + an-2.xn-2 + … + a2x2 + a1x + a0. Onde an, an-1, an-2, …, a2, a1, a0 são números reais chamados coeficientes.

O que é polinômio

Ou seja, podemos definir polinômios como expressões algébricas formadas por números (coeficientes) e letras (partes literais). As letras são utilizadas porque representam valores desconhecidos da expressão.

Os polinômios se encontram em um âmbito da matemática denominado álgebra, que correlaciona o uso de letras  representativas de um número qualquer, com operações aritméticas. Portanto, podemos utilizá-los para efetuar  operações aritméticas como adição, subtração, divisão, multiplicação, potenciação e radiciação.

Apesar de os polinômios formarem um plano conceitual importante na álgebra, também são muito relevantes para a geometria. São utilizados quando se deseja calcular expressões que envolvam valores desconhecidos.

Monômios

A definição de polinômio abrange diversas áreas, pois podemos ter polinômios com apenas um termo na expressão algébrica. Nesses casos, classificamos as expressõs como monômios.

Veja alguns exemplos: 2x, y, 4z, 2, 5

Quando existe mais de um termo em uma expressão, chamamos de polinômios. Para você compreender melhor, pense o seguinte: ‘poli’ quer dizer ‘muitos’. ‘Monômios’ quer dizer ‘termos’.

Então, um polinômio é caracterizado por conter uma série de termos (ou monômios) expressos em forma matemática.

Por exemplo:  P(x)=a_n xⁿ+a_(n-1) x^(n-1)+…+a₂ x²+a₁ x+a₀

Ainda tá difícil entender o que é um polinômio? Então veja a videoaula do Curso Enem Gratuito para acabar com as dúvidas:

Grau de um polinômio

Grau de um polinômio é o valor do maior expoente que ele possui.  Indicamos esse valor da seguinte forma: grd.(P)=n.

• Veja os exemplos para entender melhor:
• P(x) = 3x + 5 é um polinômio do 1º grau, isto é, gr(P)= 1.
• P(x) = 4x⁵ + 7 . 4 é um polinômio do 5º grau, isto é, gr(P)= 5.
• P(x) = 3x² + 2x +1 é um polinômio do 2º grau, gr(P)= 2.

Adição de polinômios

A partir daqui, vamos ver como realizar operações com polinômios. Veremos as quatro operações aritméticas: adição, subtração, multiplicação e divisão. Começaremos pela adição.

Considere os polinômios –2x² + 5x – 2 e –3x³ + 2x – 1.  Vamos efetuar, passo a passo, a adição deles.

• (–2x² + 5x – 2) + (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
•  –2x² + 5x – 2 – 3x³ + 2x – 1 → reduzir os termos semelhantes
•  –2x² + 7x – 3x³ – 3 → ordenar de forma decrescente de acordo com a potência
•  –3x³ – 2x² + 7x – 3

Subtração de polinômios

Vamos utilizar os mesmos polinômios do exemplo anterior para fazer a subtração. Basicamente, os passos são os memos. O que muda é o sinal entre os dois polinômios:

• (–2x² + 5x – 2) – (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
•  –2x² + 5x – 2 + 3x³ – 2x + 1 → reduzir os termos semelhantes
•  –2x² + 3x – 1 + 3x³ → ordenar de forma decrescente de acordo com a potência
•  3x³ – 2x² + 3x – 1

Multiplicação de polinômio por polinômio

Para efetuarmos a multiplicação de polinômio por polinômio, devemos utilizar a propriedade distributiva. Veja o exemplo:

•  (x – 1) . (x² + 2x – 6)
•  x.x² + x.2x – x.6 + (-1).x² + (-1).2x – (-1).6
•  x³ +2x² – 6x – x² – 2x + 6 → reduzindo os termos semelhantes.
•  x³ + x² – 8x + 6

Caso você tenha ficado confuso com os cálculos do primeiro passo, veja a imagem abaixo:

Antes de seguir para a operação de divisão, veja esta aula do prof. Sarkis do canal do Curso Enem Gratuito para tirar suas dúvidas sobre as operações vistas até aqui!

Divisão de polinômios

Se você está achando esse conteúdo simples, respira fundo que o verdadeiro desafio é fazer a divisão de polinômios. Apesar de ser uma operação complexa, é importante você estudar este conteúdo porque ele aparece bastante em questões de vestibulares. Vamos desvendar esse problema?

Sejam dois polinômios P(x) e D(x), com D(x) não nulo, efetuar a divisão de P por D é determinar dois polinômios Q(x) e R(x), que satisfaçam as duas condições abaixo:

• 1ª: Q(x).D(x) + R(x) = P(x)
• 2ª: gr(R) < fr(D) ou R(x) = 0.

Veja nessa divisão:

• P(x) é o dividendo;
• D(x) é o divisor;
• Q(x) é o quociente;
• R(x) é o resto da divisão.
• Quando temos R(x) = 0, dizemos que a divisão é exata, ou seja, P(x) é divisível por D(x) ou D(x) é divisor de P(x).

Exemplo de divisão

Tá difícil? Vamos ver um exemplo para decifrar essa operação. Vamos dividir 5x³ – 4x² + 3x + 1 por x² – 1. Nesse caso, 5x³ – 4x² + 3x + 1 é o P(x) ou dividendo, e x² – 1 é o D(x) ou divisor. Veja:

 

Para efetuar essa operação, dividimos sempre o primeiro termo do dividendo pelo primeiro termo do divisor. Dessa forma, o resultado será 5x, como você pode ver abaixo:

 

Assim, 5x será o primeiro termo do quociente: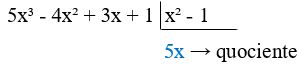

 

• Em seguida, você deve multiplicar o valor do quociente (5x) pelo valor do divisor (x² – 1).
• Veja:   5x . (x² – 1) = 5x³ + 5x
• Em seguida, você deve subtrair esse valor (5x³ + 5x) do dividendo (5x³ – 4x² + 3x + 1).

Complicou? Veja como fazer na imagem:

É importante você perceber duas coisas na imagem. Primeiramente, que colocamos x³ embaixo de x³, e x embaixo de x. Veja na sequência:

1. O grau dos polinômios é o mesmo e por isso colocamos um embaixo do outro.
2. Em segundo lugar, os termos 5x³ e 5x se tornaram negativos porque estamos fazendo uma subtração.
3. Assim, cortamos o primeiro termo porque 5x³ – 5x³ = 0. Da mesma forma, 3x – 5x = -2x.
4. Mas, a divisão não para por aí. Nós só terminaremos a divisão quando o resto for menor do que o divisor.
5. Nesse caso, o resto (-4x² – 2x +1) é de segundo grau e o divisor (x² – 1) também é de segundo grau.
6. Isso significa que podemos continuar a fazer a divisão.

Segunda parte da divisão

Então, novamente dividimos o primeiro termo do dividendo pelo primeiro termo do divisor: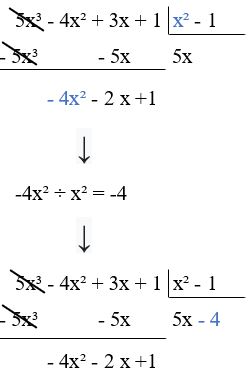

 

Da mesma forma que fizemos anteriormente, multiplicamos o valor do quociente (-4) pelo valor do divisor (x² – 1) e subtraímos do valor do dividendo (-4x² – 2x + 1):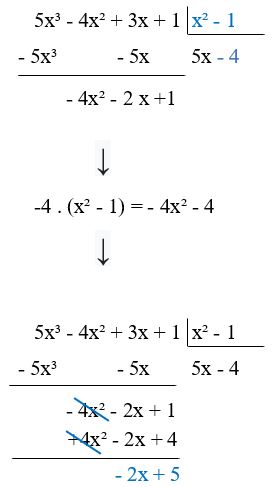Assim como fizemos anteriormente, trocamos o sinal dos termos na hora da subtração (-4x² -4 se tornou +4x² +4).

• Os polinômios de mesmo grau também ficaram um embaixo do outro (x ficou embaixo de x) e termos independentes também ficaram um embaixo do outro (+4 ficou embaixo de +1).
• Este é o momento de pararmos a divisão, pois o grau de -2x + 5 é menor do que o grau de x² – 1.
• Portanto, o quociente da divisão é 5x – 4 e o resto é -2x + 5.

Aula Gratuita: Divisão de Polinômios

Se você quiser entender melhor como fazer a divisão de polinômios, assista a esta aula do prof. Sarkis. Ele resolve o mesmo exemplo que utilizamos na aula, então vai ficar mais fácil para você entender 😉

Para entender melhor, veja alguns exercícios resolvidos sobre polinômios para complementar os seus estudos!

Exercícios sobre polinômios

Por fim, veja como o conteúdo de polinômios aparece no Enem e nos vestibulares:

1- (ENEM/2010)    

Um laticínio possui dois reservatórios de leite. Cada reservatório é abastecido por uma torneira acoplada a um tanque resfriado. O volume, em litros, desses reservatórios depende da quantidade inicial de leite no reservatório e do tempo t, em horas, em que as duas torneiras ficam abertas. Os volumes dos reservatórios são dados pelas funções V₁(t) = 250t³ – 100t + 3000 e V₂(t) = 150t³ + 69t + 3000.

Depois de aberta cada torneira, o volume de leite de um reservatório é igual ao do outro no instante t = 0 e, também, no tempo t igual a

a) 1,3 h.

b) 1,69 h.

c) 10,0 h.

d) 13,0 h.

e) 16,9 h.

2- (IFMT/2018)    

Dividindo o polinômio x³ – 4x + 3 por x – 2, encontramos o resto:

a) x + 3

b) 3

c) x – 3

d) –3

e) x² – 3

3- (ESPM SP/2016)    

O quociente e o resto da divisão do polinômio x² + x – 1 pelo binômio x + 3 são, respectivamente:

a) x – 2 e 5

b) x + 2 e 6

c) x – 3 e 2

d) x + 1 e 0

e) x – 1 e –2

GABARITO: 

1. A
2. B
3. A