Operações com Intervalos Reais – Matemática Enem

Tipos de intervalos reais: Dados dois números reais p e q, chama-se intervalo a todo conjunto de todos os números reais compreendidos entre p e q, podendo inclusive incluir p e q.

Os números p e q são os limites do intervalo, sendo a diferença p – q, chamada amplitude do intervalo. Se o intervalo incluir p e q, o intervalo é fechado e caso contrário, o intervalo é dito aberto. Viu só como dá pra entender bem os Intervalos reais? Se ficar difícil, têm as videoaulas de apoio.

A tabela abaixo define os diversos tipos de intervalos:

 

• Dica importante: (Tipos de notação para intervalos)
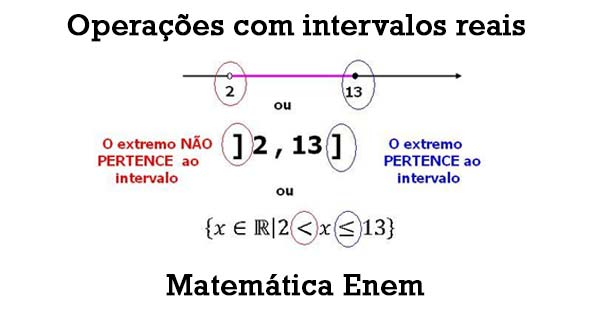
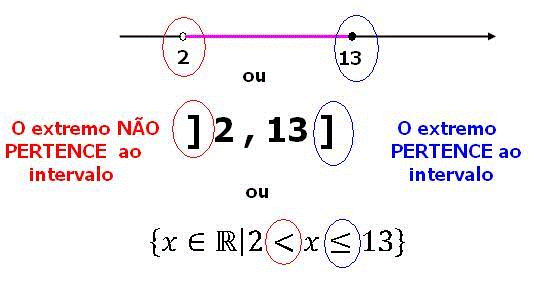
• – Notação de um intervalo na reta real com “bolinha fechada” – inclusão de termos;
• –  “bolinha aberta” – exclusão de termos.
• Você também pode verificar através da notação de intervalos ou de conjuntos através dos colchetes (intervalo fechado) e colchetes invertido (intervalo aberto) e a notação algébrica de conjuntos.

Veja agora na imagem abaixo:

Resumo sobre “Pertence” e “Não Pertence”

Confira agora com o professor Lucas Borguesan um resumo que vai ajudar demais pra você dominar este conteúdo.

As dicas do professor Lucas:

• Quem nunca se confundiu na hora de fazer operações com conjuntos numéricos, não é mesmo?
• Muitas vezes, por se tratarem de conjuntos de muitos elementos, alguns alunos podem se atrapalhar na hora de realizar as operações, como a União e a Intersecção.
• Realmente é preciso bastante atenção para não deixar nenhum elemento do conjunto numérico de lado na hora da operação.
• Mas, com um pouco de paciência, muito estudo e treinamento, pode aparecer qualquer conjunto numérico que você vai saber direitinho o que fazer com ele.
• Então, veja no resumo acima, no vídeo, como resolver estas operações e mandar bem no Enem.

 

• Concluo a classificação dos intervalos com a seguinte pergunta para vocês:
• – E o intervalo vazio, como seria definido?
• Pense um pouco….

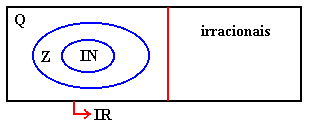
Veja a Relação entre os Conjuntos Numéricos:

• O diagrama mostra a relação entre os conjuntos numéricos. Portanto, os números naturais, inteiros, racionais e irracionais são todos números reais. Como subconjuntos importantes de IR temos:
• IR* = IR-{0}
• IR₊ = conjunto dos números reais não negativos
• IR_ = conjunto dos números reais não positivos

 

Obs: Entre dois números inteiros existem infinitos números reais. Por exemplo:

• Entre os números 1 e 2 existem infinitos números reais:
• Entre os números 5 e 6 existem infinitos números reais:

5,01 ; 5,02 ; 5,05 ; 5,1 ; 5,2 ; 5,5 ; 5,99 ; 5,999 ; 5,9999 …

Resumo sobre Conjuntos Numéricos

Confira agora com o professor Lucas Borguesan as dicas básicas sobre Conjuntos Numéricos

Veja as dicas di Professor Lucas:

1. Sabe aqueles grupinhos característicos que tem em todo ensino médio?
2. Vamos pensar juntos: toda escola tem aquele grupo que é mais bagunceiro, a galera do fundão, o pessoal mais dedicado e estudioso, a galera mais ligada em rede social, os que tocam algum instrumento…
3. Enfim, são muitos os grupinhos.
4. Mas, sabe o que todos esses grupos tem em comum? Os membros de cada grupo têm características parecidas, por isso se identificam!
5. Aqueles que têm características parecidas formam conjuntos e na matemática nós chamamos de conjuntos numéricos!

 

Intervalos Reais

• Considere para os Intervalos em R:
• Nem toda solução de um problema matemático é um número.
• Muitas vezes essa solução é um conjunto numérico contido em  (conjunto dos reais).

Vamos ver a definição…

Considere dois números reais a e b, com a<b.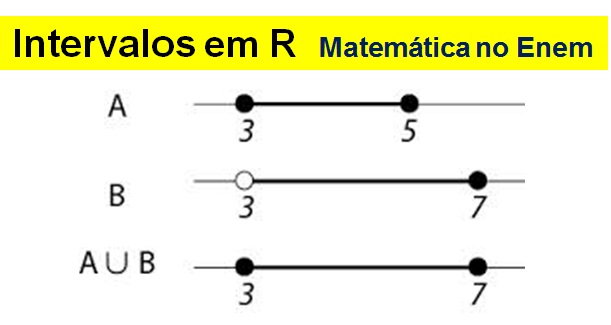 

I) Intervalo aberto de extremos a e b

• É o conjunto ]a,b[ = { x ∈ R / a < x < b }  .
• Além da representação ]a,b[  também utilizamos (a,b).
• Geometricamente representamos assim:

Dica – Você notou que nesse intervalo as bolas que o representam são abertas? Sabe o que isso significa? 

Isso significa que os números representados no intervalo por a e b, não fazem parte da solução do problema!  Agora vamos ver um outro caso:

II) Intervalo fechado de extremos a e b

• É o conjunto [a,b] = { x ∈ R / a ≤  x  ≤ b }.
• Geometricamente representamos

Como intervalos são conjuntos é natural que as operações mencionadas possam ser realizadas. E, trata-se de um procedimento muito comum na resolução de alguns problemas.

E a maneira mais fácil e intuitiva de realizar essas operações é através da representação gráfica dos intervalos envolvidos.

Em diversas situações a resolução de problemas depende de operações com intervalos, como a união, a intersecção e a diferença.

Dica de Matemática do Blog do Enem:

Veja os 10 Temas de Matemática que mais caem no Enem – Todo ano o Exame Nacional do Ensino Médio traz questões de Regra de Três; Cálculos de Área, de Ângulos, de Lados e de Perímetro em figuras planas, Calculos de Volume e de Aresta em Figuras Geométricas; Equações de 1º Grau e de 2º Grau; e mais cinco temas frequentes.

Veja a lista completa com aulas gratuitas de todos eles. Confira aqui os top 10 da Matemática no Enem. 

 Veja os Planos de Estudo Completos para o Enem:

• Os 10 Temas que mais caem no Enem
• Plano de Estudos de Português
• Plano de Estudos de Biologia
• Plano de Estudos de Química
• Plano de Estudos de Geografia
• Plano de Estudos de História
• 10 Passos para Redação Enem nota mil
• Plano de Estudos de Matemática

Os Intervalos reais

Definição teórica de União, Intersecção e Diferença de Intervalos

Para fazer estas operações (união, intersecção) devemos:

• Marcar sobre uma mesma reta, em ordem crescente, todos os números que são extremos dos intervalos;

• Abaixo da reta traçamos os intervalos que representam os conjuntos, usando “bolinha aberta” para a exclusão do extremo e “bolinha fechada” para a inclusão dos extremos;

•  Os trechos comuns dos intervalos determinam a intersecção e os trechos que estão em pelo menos um dos intervalos indicam a união.

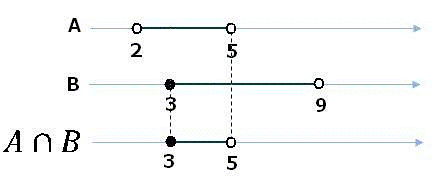
Vamos ver um exemplo de União de intervalos

 

Propriedades dos Intervalos Reais

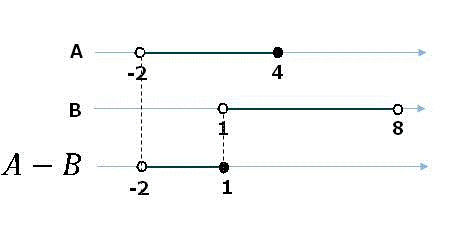
Solução. Observando os intervalos e seus limites na reta numérica, temos:

 

OBS: 1) Na intersecção os extremos são excluídos porque 2 não está em B e 3 não está em A.

          2) Na diferença a extremidade 2 está inclusa porque não pertence ao conjunto B.

Resposta: alternativa a

 

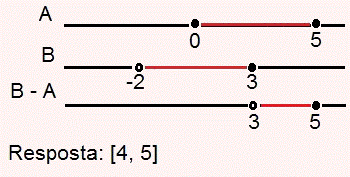
A alternativa correta para essa questão é a letra c.

Os textos e exemplos acima foram preparados pela professora Jaceli Eccher para o Blog do Enem. Jaceli é formada em Matemática habilitação Licenciatura pela Universidade Federal de Santa Catarina com Especialização no ensino de Ciências pelo Instituto Federal de Santa Caratina. Facebook: https://www.facebook.com/Jacelieccher