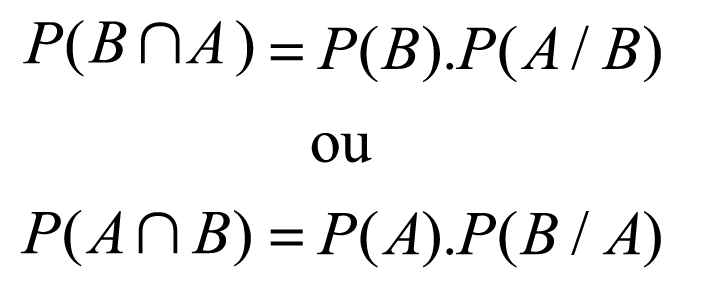Garanta o sucesso no Enem com este resumo sobre sobre Probabilidade. Veja aula gratuita com o professor Sérgio Sarkis, e depois responda as 10 questões do simulado de Matemática que preparamos para você. Se errar, têm dicas para estudar!
Probabilidade é um tema frequente no Enem e nos vestibulares. Então, para mandar bem nas provas, preparamos um simulado para você ver o que sabe. Mas antes, veja este resumo sobre o tema, serão contempladas situações que envolvem experimentos aleatórios, cuja teoria probabilística estabelece e estuda as possibilidades de ocorrência.
Para resolver problemas de probabilidade de um evento condicionado à ocorrência de um outro a estratégia para mandar bem é utilizar a famosa Probabilidade Condicional, cuja fórmula é dada por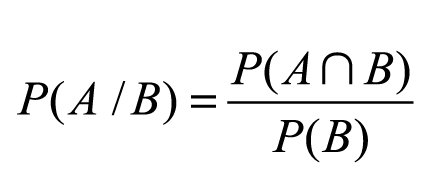 em que P(A/B) representa a probabilidade de ocorrência do evento A, dado que já ocorreu B.
em que P(A/B) representa a probabilidade de ocorrência do evento A, dado que já ocorreu B.
- Nesta fórmula, isolando P(A∩B), obtemos

- que é equivalente a

O que é Probabilidade
Veja agora com o professor Lucas Borguesan, do canal do Curso Enem Gratuito.
Observação importante:
- Costumamos chamar essa fórmula de Regra do Produto
- Quando a ocorrência do evento B afetar a probabilidade do evento A, dizemos que os eventos A e B são Dependentes. Quando não afetar, serão chamados de Independentes e, neste caso, a fórmula será dada por

Veja a seguir Exemplos de exercícios resolvidos bem típicos, que sempre caem, envolvendo jogo de dados e lançamentos de moedas para tirar no “cara ou coroa”. Se liga:
01 – Lançando simultaneamente um dado e uma moeda, qual a probabilidade de obtermos o número 4 no dado e “cara” na moeda?
Resolução de Probabilidade
Considere os eventos:
- A: número 4 no dado ⇒ P(A) = 1/6
- B: cara na moeda ⇒ P(B) = 1/2.
Queremos calcular P(A∩B). Pela fórmula,
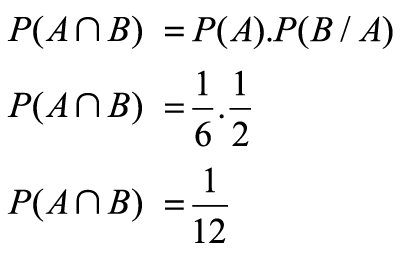
Perceba que o fato de ter saído cara na moeda não altera a probabilidade de sair o número 4 no dado. Logo, são eventos independentes.
Aula Gratuita sobre Probabilidade – Veja!
Confira com o professor Sérgio Sarkis, do canal Curso Enem Gratuito, um resumo simples e rápido com o que você precisa aprender de Probabilidade para resolver as questões das provas.
Muito boa esta explicação do professor Sarkis. Agora, vamos com a aula completa:
Estudando probabilidade com outras situações
- Considere os seguintes experimentos:
- a) – Aquecimento de água contida em uma panela;
- b ) Queda livre de um corpo.
- Conhecidas certas condições, podemos prever a temperatura em que a água entrará em ebulição e à velocidade com que o corpo atingirá o solo.
Os experimentos cujos resultados podem ser previstos, são denominados experimentos determinísticos.
Consideremos também os experimentos:
- –Lançamento de uma moeda e leitura da figura da face voltada para cima.
- – Lançamento de um dado e leitura do número voltado para cima.
- – Nascimento de uma criança.
- – Sorteio de uma carta de baralho.
Mesmo que estes experimentos fossem repetidos várias vezes, nas mesmas condições, não seria possível prever o seu resultado. Estes experimentos são denominados experimentos aleatórios.
A teoria das probabilidades estuda a forma de estabelecer as possibilidades de ocorrência destes experimentos.
Em nosso cotidiano, é frequente ouvirmos frases como “a probabilidade de chover amanhã é de mais 25%”, “a probabilidade de que ocorram acidentes nas rodovias seria menos se as leis de trânsito fossem respeitadas” ou “a probabilidade de que haja reduções de preço é remota”.
Além dessas, existem muitas outras situações em que são utilizados cálculos para determinar as chances de que certo acontecimento ocorra.
Um meteorologista, por exemplo, a partir de algumas informações, pode calcular a probabilidade de que ocorram chuvas em determinada região nas próximas horas. Outra situação é a determinação do valor do seguro de um bem, que é calculado levando em consideração a probabilidade de perda ou avaria desse bem.
Probabilidade
Experimento Aleatório
São fenômenos que, mesmo repetidos várias vezes sob condições semelhantes, apresentam resultados imprevisíveis. O resultado final depende do acaso.
Exemplo:
Da afirmação “é provável que o meu time ganhe a partida hoje” pode resultar:
– que ele ganhe – que ele perca – que ele empate
Este resultado final pode ter três possibilidades.
Espaço Amostral
- É o conjunto universo ou o conjunto de resultados possíveis de um experimento aleatório.
- No experimento aleatório “lançamento de uma moeda” temos o espaço amostral {cara, coroa}.
- No experimento aleatório “lançamento de um dado” temos o espaço amostral {1, 2, 3, 4, 5, 6}.
- No experimento aleatório “dois lançamentos sucessivos de uma moeda” temos o espaço amostral :
- {(ca,ca) , (co,co) , (ca,co) , (co,ca)}
- Obs: cada elemento do espaço amostral que corresponde a um resultado recebe o nome de ponto amostral. No primeiro exemplo: cara pertence ao espaço amostral {cara, coroa}.
Exercício Resolvido de Probabilidade
Confira agora uma questão de prova resolvida, onde você precisa aplicar os conhecimentos de Probabilidade. É simples de entender. Acompanhe com o professor Sérgio Sarkis
Viu como é simples de resolver? Confira agora o que são os “Eventos” na Probabilidade:
Eventos
É qualquer subconjunto do espaço amostral de um experimento aleatório.
Se considerarmos S como espaço amostral e E como evento: Assim, qualquer que seja E, se E c S (E está contido em S), então E é um evento de S.
Se E = S , E é chamado de evento certo.
Se E ![]() S e E é um conjunto unitário, E é chamado de evento elementar.
S e E é um conjunto unitário, E é chamado de evento elementar.
Se E = Ø , E é chamado de evento impossível.
Conceito de probabilidade
Chamamos de probabilidade de um evento A (sendo que A está contido no Espaço amostral) o número real P(A) , tal que : número de casos favoráveis de A / número total de casos
OBS: Quando todos os elementos do Espaço amostral tem a mesma chance de acontecer, o espaço amostral é chamado de conjunto equiprovável.
Exemplos:
1- No lançamento de uma moeda qual a probabilidade de obter cara em um evento A ?
S = { ca, co } = 2 A = {ca} = 1 P(A) = 1/2 = 0,5 = 50%
2- No lançamento de um dado qual a probabilidade de obter um número par em um evento A ?
S = { 1,2,3,4,5,6 } = 6 A = { 2,4,6 } = 3 P(A) = 3/6 = 0,5 = 50%
3- No lançamento de um dado qual a probabilidade de obter um número menor ou igual a 6 em um evento A ?
S = { 1,2,3,4,5,6 } = 6 A = { 1,2,3,4,5,6 } = 6 P(A) = 6/6 = 1,0 = 100%
Obs: a probabilidade de todo evento certo = 1 ou 100%.
4- No lançamento de um dado qual a probabilidade de obter um número maior que 6 em um evento A ?
S = { 1,2,3,4,5,6 } = 6 A = { } = 0 P(A) = 0/6 = 0 = 0%
Obs: a probabilidade de todo evento impossível = 0 ou 0%
Teste agora o seu nível com o simulado Enem de Matemática:
Probabilidade – Simulado Enem de Matemática
.
Venha para o Curso Enem Gratuito:
Criamos para você duas novidades: Um Curso Enem Online totalmente gratuito, e uma bateria de Simulados Enem Gratuitos, com todas as matérias do Exame Nacional do Ensino Médio. Acesse o Curso e faça os Simulados para chegar bem no próximo Enem! Simulados com Gabarito na mesma hora. Veja aqui:
Você pode estudar uma aula gratuita por dia no Curso Enem Online, com todas as matérias do Exame Nacional do Ensino Médio e também as Dicas para uma Redação Enem Nota 1000. Na verdade você pode estudar quantas aulas quiser por dia. Mas, o importante é criar o hábito de ver pelo menos uma aula por dia.

Simulado Enem Online – Escolha a sua próxima prova:
Biologia
- 1. 10 questões sobre vitaminas: simulado de Biologia
- 2. A Evolução das Espécies: resumo de Biologia com Simulado
- 3. A Primeira Lei de Mendel. Resumo com Simulado de Genética
- 4. As funções da Água no Corpo Humano: resumo e simulado
- 5. As Relações Ecológicas – Resumo Enem & Encceja com Simulado
- 6. Características Básicas dos Seres Vivos: resumo com simulado
- 7. Carboidratos – Resumo Enem com Simulado Online de Biologia
- 8. Covid-19, a volta do Sarampo e a crise das vacinas no Brasil
- 9. Cromatina, cromossomos e cariótipo: resumo de Biologia Enem
- 10. Divisão Celular – Resumo de Meiose & Mitose com Simulado
- 11. Enzimas: Resumo com Simulado de Biologia Enem & Encceja
- 12. Exercícios sobre Darwinismo e Lamarckismo
- 13. Exercícios sobre fermentação alcoólica e láctica
- 14. Exercícios sobre membrana plasmática e transportes passivo e ativo
- 15. Intérfase – Resumo de Biologia Enem com Simulado
- 16. Lipídios na Biologia do Enem & do Encceja: resumo com Simulado Online
- 17. Lista de exercícios sobre DNA e RNA – Biologia Enem
- 18. Lista de exercícios sobre genética, com resumo de revisão
- 19. Lista de exercícios sobre respiração celular
- 20. Meiose – Resumo com Simulado de Biologia Enem & Encceja
- 21. Métodos Científicos x Senso Comum: resumo com Simulado Enem
- 22. Métodos Contraceptivos e mais 10 Temas de Biologia Enem
- 23. Métodos Contraceptivos: resumo e simulado Enem de biologia
- 24. Mitocôndria e Energia Celular: resumo Enem & Encceja de Biologia
- 25. Mitose – Revisão e Simulado Enem de Biologia com 10 questões
- 26. O que são os Cromossomos: resumo sobre DNA & RNA
- 27. Os seis Biomas Brasileiros: resumo de Geografia com Simulado Enem
- 28. Os tipos de Microscópios: resumo Enem com simulado
- 29. Questões do Enem sobre a Malária e doenças virais
- 30. Questões sobre evolução das espécies
- 31. Questões sobre organelas celulares
- 32. Questões sobre proteínas a aminoácidos com resumo de Biologia
- 33. Reprodução Assexuada – Resumo de Biologia Enem com Simulado
- 34. Resumo com lista de exercícios sobre Relações Ecológicas
- 35. Sais Minerais: resumo de Biologia Enem com Simulado
- 36. Simulado Enem de Biologia – Os temas que mais caem
- 37. Simulado grátis de Matemática Enem com nota pela TRI
- 38. Sucessão Ecológica – Simulado Enem com aula de revisão gratuita. Veja!
- 39. Teorias sobre a Origem da Vida: resumo com Simulado Enem
- 40. Veja o que são as Proteínas: resumo de biologia Enem
- 41. Veja o Transporte Passivo da Osmose na Membrana Plasmática
- 42. Vírus Ebola – Resumo Enem & Encceja com dicas e simulado online
- 43. Zika Vírus e Microcefalia: resumo de Biologia com simulado
Filosofia
- 1. Exercícios sobre Escola de Frankfurt
- 2. Exercícios sobre os filósofos da natureza
- 3. Filósofos da Natureza – Resumo com Simulado Enem & Encceja
- 4. Homem, um animal político: veja o pensamento de Aristóteles
- 5. Indústria Cultural: resumo com Simulado Enem de Sociologia
- 6. Jean-Jacques Rousseau e o Iluminismo: resumo de filosofia
- 7. Lista de questões sobre Immanuel Kant
- 8. O Mito da Caverna de Platão – Simulado de Filosofia
- 9. O Pensamento Mítico – Resumo de Filosofia Enem com Simulado
- 10. O que é a Filosofia – aula gratuita com Simulado Enem & Encceja
- 11. O que são os Mitos – Resumo com Simulado Enem de Filosofia
- 12. Os Filósofos do Iluminismo e a origem da Revolução Francesa
- 13. Os Filósofos Sofistas – Resumo com Simulado Enem & Encceja
- 14. Platão e as formas de governo: resumo com Simulado Enem
- 15. Platão e as ideias de justiça e política: resumo com exercícios
- 16. Platão e o Mundo das Ideias: resumo de Filosofia com simulado
- 17. Questões sobre ética
- 18. Questões sobre existencialismo
- 19. Questões sobre Nicolau Maquiavel. Resumo com simulado
- 20. Questões sobre René Descartes e o Racionalismo
- 21. Questões sobre Rousseau: o Iluminismo e a Revolução Francesa
- 22. Questões sobre Thomas Hobbes
- 23. Resumo e Simulado sobre a filosofia de Aristóteles
- 24. Sócrates e o Oráculo de Delfos: resumo de Filosofia Enem
- 25. Sócrates e o Pensamento Sofista: resumo Enem de Filosofia
- 26. Veja os Filósofos da Natureza – Resumo de Filosofia Enem
Física
- 1. 10 questões sobre as Leis de Newton
- 2. A origem da Física como ciência: resumo Enem com Simulado
- 3. A primeira lei da termodinâmica: resumo com simulado de Física
- 4. Acústica: lista de exercícios do Enem e vestibulares
- 5. Definição e Soma de Vetores: veja resumo com Simulado Enem
- 6. Equilíbrio de Corpo Extenso – Simulado de Física
- 7. Exercícios sobre energia cinética: velocidade e aceleração
- 8. Exercícios sobre fenômenos ondulatórios
- 9. Exercícios sobre óptica geométrica
- 10. Exercícios sobre transmissão de calor
- 11. Força Atrito – Simulado Enem Online de Física com 10 questões
- 12. Grandezas vetoriais e escalares: resumo de Física com simulado
- 13. Hidrostática: resumo online de Física com Simulado Enem
- 14. Impulso e Quantidade de Movimento – Simulado de Física Enem
- 15. Lançamento de Peso – Simulado Enem Online de Física com 10 questões
- 16. Lista de exercícios sobre as 3 Leis de Newton
- 17. Lista de exercícios sobre calorimetria, com resumo de física
- 18. Lista de exercícios sobre ondulatória
- 19. Lista de exercícios sobre potência elétrica
- 20. Movimento Circular Uniforme: resumo com Simulado de Física
- 21. Movimento Retilíneo Uniforme + MRUV: resumo com simulado
- 22. MRU + MRUV: resumo online com Simulado Enem de Física
- 23. O Princípio de Arquimedes: resumo de Física com Simulado
- 24. Óptica – Resumo com Simulado Enem de Física
- 25. Queda Livre + MRU – Veja resumo com Simulado Enem & Encceja de Física
- 26. Repouso e Movimento: aprenda Física com resumo e simulado
- 27. Resolução de questões de Circuitos Elétricos: Física Enem
- 28. Resumo com lista de exercícios sobre Movimento Uniforme
- 29. Resumo da 1ª Lei da Termodinâmica, com Simulado Enem de Física
- 30. Resumo de Física sobre Escalas Termométricas, com simulado
- 31. Simulado de Física Básica do Enem – Teste seu nível em 10 questões
- 32. Sistema Internacional de Unidades (SIU) – Simulado Enem
- 33. Sistemas conservativos – Simulado de Física com 10 questões
- 34. Soma de Vetores – Resumo Online de Física com Simulado Gratuito
- 35. Transmissão de Calor – Simulado Enem Online de Física com 10 questões
- 36. Velocidade – Simulado Enem Online de Física com 10 questões
- 37. Velocidade, Aceleração, Tempo e Espaço. Simulado de Física – Cinemática
Geografia
- 1. 10 vezes que a Ucrânia caiu no Enem e vestibulares
- 2. A Deriva Continental e o movimento das Placas Tectônicas
- 3. A Divisão Política do Brasil: resumo com simulado de Geografia
- 4. A história geológica da Terra: resumo com simulado Enem
- 5. A Posição Geográfica do Brasil: resumo Enem com Simulado
- 6. A Rosa dos Ventos e os 4 Pontos Cardeais: resumo com simulado
- 7. Aquecimento Global: resumo com Simulado Enem & Encceja
- 8. As Camadas da Atmosfera: resumo & simulado de geografia Enem
- 9. As Eras Geológicas – Resumo Online com Simulado Enem de Geografia
- 10. Características do Continente Europeu: resumo e simulado Enem
- 11. Comércio Exterior – Simulado Enem Online de Geografia com 10 questões
- 12. Continente Africano: Resumo com Simulado de Geografia Enem
- 13. Crosta terrestre ou litosfera: resumo com imulado de Geografia
- 14. Escala Cartográfica – Resumo enem de Geografia com Simulado
- 15. Espaço rural brasileiro – Resumo de Geografia Enem com Simulado
- 16. Exercícios sobre as fontes de energia e a matriz energética no Brasil
- 17. Exercícios sobre degradação ambiental
- 18. Exercícios sobre formação e degradação do solo
- 19. Fusos Horários no Brasil – Resumo com Simulado Enem de Geografia
- 20. GPS – Resumo com Simulado Enem de Geografia
- 21. Impacto Ambiental: resumo com simulado de Geografia. Vem!
- 22. Latitude e Longitude: resumo com simulado de Geografia
- 23. Lista de exercícios sobre a indústria brasileira
- 24. Lista de exercícios sobre globalização
- 25. Lista de exercícios sobre hidrografia para o Enem
- 26. Lista de exercícios sobre urbanização brasileira
- 27. Lista de questões sobre a Otan
- 28. Lista de questões sobre cartografia
- 29. O Movimento de Rotação da Terra- Resumo Enem com Simulado
- 30. O Sistema Solar e a ordem dos planetas: resumo com simulado
- 31. Origem do Universo – Simulado Enem de Geografia com 10 questões
- 32. Placas Tectônicas: tsunamis, vulcões e terremotos: resumo Enem
- 33. Projeções cartográficas cilíndricas: resumo com simulado Enem
- 34. Questões sobre clima e climatologia
- 35. Recursos minerais – Simulado Enem Online de Geografia com 10 questões
- 36. Resumo com Simulado de Geografia: os 10 temas que mais caem
- 37. Resumo de Geologia Geral com simulado Enem de Geografia
- 38. Resumo de Hidrosfera, com Simulado de Geografia Enem
- 39. Tipos de rochas – Simulado Enem de Geografia com 10 questões
- 40. Veja o Movimento de Translação da Terra ao redor do Sol
Gramática
- 1. 10 questões sobre coesão textual na redação do Enem
- 2. 10 questões sobre Figuras de Linguagem
- 3. 10 questões sobre formação de palavras
- 4. A Função do Advérbio: resumo com simulado de Gramática
- 5. A Morfologia das Palavras no Português: resumo Enem
- 6. Adjetivos – Resumo com Simulado Enem de Português
- 7. Artigos Definidos e Artigos Indefinidos: resumo de Gramática
- 8. As sílabas tônicas: resumo de Gramática com simulado
- 9. Cognatos, homônimos e parônimos – Revisão e Simulado Enem de Gramática
- 10. Conjunções Adverbiais – Resumo com Simulado Enem de Gramática. Veja!
- 11. Exercícios sobre os usos da vírgula
- 12. Exercícios sobre termos acessórios da oração: adjuntos, aposto e vocativo
- 13. Interpretação de Textos e de Tirinhas – Resumo com Simulado
- 14. Lista de exercícios sobre acentuação gráfica
- 15. Lista de exercícios sobre conotação e denotação
- 16. Lista de exercícios sobre formação de palavras
- 17. Lista de exercícios sobre prefixo e sufixo
- 18. Modo indicativo: resumo de português com simulado Enem
- 19. Modo Verbal (Subjuntivo e Imperativo): resumo e simulado de gramática
- 20. O uso do Gerúndio – Resumo simulado Enem gratuito
- 21. Oração Subordinada: simulado Enem com resumo de Português
- 22. Ortografia: o uso das letras – Simulado Enem Online de Gramática com 10 questões
- 23. Os 5 Tipos de Sujeito – Resumo e simulado Enem de Português
- 24. Prefixos e Sufixos – Resumo com Simulado Enem & Encceja de Gramática
- 25. Pronomes e elementos de coesão – Simulado Enem de Gramática
- 26. Pronomes retos, oblíquos e demonstrativos: resumo com Simulado
- 27. Questões de interpretação de texto: dicas de português Enerm
- 28. Recursos Ortográficos e Efeitos de Sentido: resumo com simulado
- 29. Resumo com exercícios sobre linguagem verbal e não verbal
- 30. Resumo com lista de exercícios sobre as funções da linguagem
- 31. Resumo com simulado de Acentuação Gráfica: Português Enem
- 32. Resumo de Acentuação Gráfica com Simulado Enem de Gramática
- 33. Resumo de Divisão Silábica com simulado Enem de Português
- 34. Resumo de Fonemas, com simulado de Português Enem
- 35. Sinais de Pontuação: veja aula gratuita com Simulado Enem de Gramática
- 36. Substantivos: resumo de Português com simulado
- 37. Variedades Linguísticas: resumo de Gramática com simulado
- 38. Veja 10 dicas de Gramática com Simulado Enem
- 39. Veja a Oração Reduzida no resumo Enem de Português
- 40. Veja os Sinônimos e os Antônimos: resumo Enem de Gramática
História
- 1. A Ditadura Militar no Brasil: resumo e simulado Enem de História
- 2. A Era Vargas de 1930 a 1945: veja as características do período
- 3. A Ideologia Nazista – Resumo com simulado de História Enem
- 4. A República Populista: Período Democrático de 1945 a 1964
- 5. A Revolução Industrial – Resumo com Simulado Enem & Encceja
- 6. A Segunda Guerra Mundial – Resumo com Simulado
- 7. Absolutismo – Resumo e Simulado de História Enem & Encceja
- 8. Antiguidade Clássica: resumo e simulado de História Enem
- 9. As Revoltas Coloniais no Brasil: resumo e simulado de História
- 10. Ciclo do café no Brasil: resumo e questões
- 11. Civilização Árabe – Resumo com Simulado Enem de História
- 12. Civilização da Mesopotâmia: resumo Enem & Encceja com Simulado de História
- 13. Civilização dos Fenícios – Resumo e Simulado de História Enem
- 14. Civilização Romana – Resumo Enem com aula gratuita e Simulado
- 15. Exercícios sobre a colonização mercantilista europeia
- 16. Exercícios sobre a sociedade colonial no Brasil
- 17. Exercícios sobre Baixa Idade Média
- 18. Exercícios sobre renascimento comercial e urbano
- 19. Exercícios sobre revoltas coloniais nativistas
- 20. Expansão Marítima e Grandes Navegações: resumo com Simulado
- 21. Grécia Antiga: lista de exercícios e resumo
- 22. História das eleições no Brasil – Resumo e questões
- 23. Império Bizantino – Simulado Enem Online de História com 10 questões
- 24. Lista de exercícios sobre a Revolução Francesa
- 25. Lista de exercícios sobre o Segundo Reinado
- 26. Mercantilismo – Resumo com Simulado Enem de História
- 27. Nova República – Simulado Enem Online de História com 10 questões
- 28. O Egito Antigo e as pirâmides dos Faraós: resumo de História
- 29. O Fascismo italiano – Resumo de HIstória com Simulado Enem
- 30. Os Hebreus – Resumo com simulado: a História dos Judeus
- 31. Os Persas: resumo com Simulado Enem de História
- 32. Pré História – Aula gratuita com Simulado Enem Online
- 33. Questões sobre a independência do Brasil
- 34. Questões sobre a vinda da família real para o Brasil
- 35. Questões sobre o ciclo da cana-de-açúcar Brasil colonial
- 36. República Velha: Aula gratuita e simulado de História
- 37. Resumo com Simulado Enem: o ciclo das Grandes Navegações
- 38. Resumo da Escravidão, Resistência, Abolição e Racismo no Brasil
- 39. Resumo da Revolução Francesa, com Simulado de História
- 40. Resumo de História e Filosofia Enem com Simulado de Iluminismo
- 41. Resumo Enem de Pré-História com dicas e Simulado
- 42. Teorias da História – Simulado Enem Online de História com 10 questões
Inglês
- 1. Adjetivos em Inglês e Interpretação de textos no Enem
- 2. Advérbios de frequência – Simulado Enem de Inglês com 10 questões
- 3. Apóstrofo – Revisão e Simulado Enem de Inglês com 10 questões
- 4. Artigo Definido – Simulado Enem Online de Inglês com 10 questões
- 5. Artigos Indefinidos: resumo com simulado de Inglês
- 6. Como interpretar textos em Inglês: resumo com simulado Enem
- 7. Conditionals – Simulado Enem de Inglês com 10 questões
- 8. Exercícios sobre verbos regulares e irregulares
- 9. Inglês no Enem: dicas sobre os Nouns. Resumo com Simulado
- 10. Interpretação de texto em inglês: veja as técnicas de Skimming e Scanning
- 11. Interrogative Pronouns: resumo com simulado Enem de Inglês
- 12. Nominal Groups – Simulado Enem Online de Inglês com 10 questões
- 13. Prepositions – Resumo com Simulado Enem de Inglês
- 14. Present Continuous no Inglês: resumo com simulado Enem
- 15. Present Perfect no Inglês: resumo com simulado Enem
- 16. Pronomes em Inglês: veja no resumo com simulado Enem
- 17. Pronomes Indefinidos – Simulado Enem de Inglês com 10 questões
- 18. Pronomes Relativos em Inglês: veja no resumo com simulado
- 19. Quantificadores – Resumo com simulado de Inglês Enem
- 20. Question Words: veja um resumo com simulado Enem de Inglês
- 21. Questões sobre interpretação de músicas e poemas em inglês
- 22. Questões sobre interpretação de texto em inglês com gabarito
- 23. Simple Present – Aula gratuita com Simulado Enem
- 24. Singular e Plural – Resumo de Inglês com dicas e simulado
- 25. Substantivos Contáveis e Incontáveis – Simulado Enem de Inglês
- 26. Veja o verbo To Be: resumo com simulado Enem de Inglês
Literatura
- 1. As Características do Romantismo: resumo Enem & Encceja
- 2. As funções da Arte Literária: resumo Enem com Simulado Online
- 3. As Funções da Linguagem – Resumo com Simulado de Literatura
- 4. Classicismo – Resumo com Simulado de Literatura Enem & Encceja
- 5. Exercícios sobre Clarice Lispector, com resumo de literatura
- 6. Exercícios sobre o Simbolismo no Brasil
- 7. Gênero Dramático – Resumo com Simulado Enem de Literatura
- 8. Gêneros Literários – Revisão Online com Simulado de Literatura
- 9. Intertextualidade: Resumo de Literatura Enem com Simulado
- 10. Linguagem Denotativa x Conotativa: resumo com simulado Enem
- 11. Lista de exercícios sobre figuras de linguagem
- 12. Lista de exercícios sobre o Realismo no Brasil
- 13. Naturalismo – Resumo de Literatura Enem com Simulado
- 14. O Arcadismo na literatura do Enem: resumo com Simulado
- 15. O que é Metalinguagem: veja no resumo Enem de Literatura
- 16. O Quinhentismo: resumo com simulado de Literatura Enem
- 17. O Romantismo e a Poesia pela Liberdade e contra a Escravidão
- 18. O Romantismo na literatura brasileira: resumo com simulado
- 19. Os Tipos Textuais: resumo sobre o estilo da Redação Enem
- 20. Parnasianismo – Resumo com Simulado de Literatura
- 21. Questões sobre a primeira fase do Modernismo no Brasil
- 22. Questões sobre a Segunda Fase do Modernismo
- 23. Questões sobre música no Enem e vestibulares
- 24. Questões sobre Pré-Modernismo – Exercícios de Literatura
- 25. Questões sobre terceira fase do Modernismo
- 26. Resumo com exercícios sobre o Romantismo no Brasil
- 27. Resumo das Vanguardas Europeias, com simulado Enem
- 28. Resumo e lista de exercícios sobre Machado de Assis
- 29. Resumo sobre Função Poética da Linguagem: literatura Enem
- 30. Revisão – Simulado Enem Online de Literatura com 10 questões
- 31. Segunda fase do Modernismo no Brasil
- 32. Semana de Arte Moderna: literatura Enem. Resumo e Simulado
- 33. Terceira Geração Modernista – Resumo de Literatura com Simulado
- 34. Veja o Barroco em Portugal – Resumo com Simulado de Literatura
- 35. Veja o Barroco no Brasil: resumo com simulado de Literatura
Matemática
- 1. 10 questões sobre cálculo de juros simples e compostos
- 2. 10 questões sobre porcentagem: resumo com simulado
- 3. 10 questões sobre Teorema de Pitágoras e relações do triângulo retângulo
- 4. Binômio de Newton – Resumo Online com Simulado Enem Gratuito
- 5. Circunferência trigonométrica: resumo e simulado Enem
- 6. Conjuntos: resumo online com Simulado Enem & Encceja de Matemática
- 7. Critérios de Divisibilidade: resumo com Simulado de Matemática
- 8. Dedução Matemática – Simulado Enem & Encceja
- 9. Dominando a Matemática para o Enem: Aulão Especial e Simulado com Nota pela TRI
- 10. Exercícios sobre análise combinatória e Princípio Fundamental da Contagem
- 11. Exercícios sobre equação de 2º grau e fórmula de Bhaskara
- 12. Exercícios sobre figuras planas
- 13. Exercícios sobre triângulo retângulo e o Teorema de Pitágoras
- 14. Expressões algébricas – Resumo Enem de Matemática com Simulado
- 15. Função de 1º Grau: resumo com exemplos e exercícios
- 16. Função de Primeiro Grau – Resumo com Simulado Enem
- 17. Função do 1º Grau: resumo com Simulado Enem de Matemática
- 18. Juros Simples e Juros Compostos: Matemática Enem & Encceja
- 19. Leitura de gráficos e imagens: resumo com Simulado
- 20. Lista de exercícios sobre equações do 1º grau: resumo e simulado
- 21. Lista de exercícios sobre média aritmética simples e ponderada
- 22. Lista de exercícios sobre regra de três
- 23. Lista de exercícios sobre sistemas lineares: matemática Enem
- 24. Matemática no Enem: professor ensina como resolver as questões da prova
- 25. Média Simples e Média Ponderada: Resumo Enem & Encceja
- 26. O Ângulo e suas classificações: resumo com Simulado Enem
- 27. O Cálculo de Porcentagem: resumo com Simulado de Matemática
- 28. Os Números Complexos: resumo com Simulado Enem de Matemática
- 29. Potência de base 10 – Resumo e simulado Enem de Matemática
- 30. Potenciação – Resumo com Simulado Enem de Matemática
- 31. Probabilidade – Resumo de Matemática com Simulado Enem & Encceja
- 32. Regra de Três e Aresta: resumo com simulado Enem
- 33. Resumo com Lista de Exercícios sobre polinômios
- 34. Resumo com Lista de Exercícios sobre porcentagem
- 35. Resumo com simulado de Regra de Três Simples, e Composta
- 36. Resumo de Frações: Matemática com Simulado Enem
- 37. Resumo de Progressão Aritmética, com Simulado Enem
- 38. Resumo e exercícios sobre razão e proporção
- 39. Simulado de Notação Científica, com resumo de Matemática
- 40. Simulado grátis de Matemática Enem com nota pela TRI
- 41. Triângulos no Enem: veja o resumo com simulado gratuito
Química
- 1. A Configuração dos Elétrons: resumo Enem de Química
- 2. Ácidos e Bases: resumo de Química com Simulado
- 3. Cadeias de Carbono – Resumo com Simulado Enem de Química
- 4. Cálculo Estequiométrico – Resumo com Simulado Enem de Química
- 5. Cinética química – Simulado Enem de Química
- 6. Definição e propriedades da matéria – Simulado de Química
- 7. Diluição de Soluções – Simulado Enem Online de Química com 10 questões
- 8. Exercícios sobre concentração comum e molar de soluções
- 9. Exercícios sobre ligações químicas iônicas e covalentes
- 10. Exercícios sobre radioatividade
- 11. Exercícios sobre tabela periódica com resumo de Química
- 12. Fatores que alteram a cinética química – Simulado Enem
- 13. Fórmula Empírica e Molecular: resumo e simulado Enem
- 14. Lista de exercícios sobre compostos orgânicos
- 15. Lista de exercícios sobre eletroquímica, com resumo grátis
- 16. Lista de exercícios sobre forças intermoleculares
- 17. Modelos Atômicos – Simulado Enem com aula gratuita
- 18. Mol e Número de Avogadro: resumo com simulado
- 19. Nada se cria, nada se perde, tudo se transforma: a Lei de Lavoisier
- 20. O Átomo do Carbono – Resumo Enem com simulado de Química
- 21. O Diagrama de Fases: resumo Enem de Química com simulado
- 22. O que é fórmula molecular, fórmula empírica e fórmula mínima
- 23. Radioatividade no Enem: resumo com simullado de Química
- 24. Resumo com exercícios sobre estrutura atômica
- 25. Resumo com Exercícios sobre Química Ambiental no Enem
- 26. Resumo com Simulado Enem de Química: teste seu nível
- 27. Resumo de Química com exercícios de funções orgânicas
- 28. Simulado de Equilíbrio Químico: veja o resumo antes de responder
- 29. Sólido; Líquido; e Gasoso: os Estados físicos da matéria
- 30. Soluções Químicas no Enem: Soluto; Solvente; e Solubilidade
- 31. Tabela Periódica: resumo com simulado de Química Enem e Encceja
Espanhol
- 1. Acentuação no Espanhol – Resumo com Simulado Enem
- 2. Adjetivos – Revisão e Simulado Enem de Espanhol com 10 questões
- 3. Artículo neutro – Revisão e Simulado Enem de Espanhol com 10 questões
- 4. Artículos e Contracciones – Simulado Enem Online de Espanhol
- 5. Conjunções Subordinada. Resumo de Espanhol Enem
- 6. Gênero e número dos substantivos – Simulado Enem de Espanhol
- 7. Heterogenéricos – Simulado Enem de Espanhol com 10 questões
- 8. Heterotônicos – Resumo com Simulado Enem de Espanhol
- 9. Los demonstrativos – Simulado Enem Online de Espanhol com 10 questões
- 10. Los numerales cardinales y las horas: Simulado de Espanhol
- 11. Los posesivos – Simulado Enem Online de Espanhol com 10 questões
- 12. Números Ordinais – Simulado Enem Online de Espanhol com 10 questões
- 13. Os porquês – Resumo com Simulado Enem de Espanhol
- 14. Plural – Simulado Enem de Espanhol com 10 questões
- 15. Presente do Indicativo. Resumo com simulado Enem de Espanhol
- 16. Pronombres Interrogativos: resumo com simulado de Espanhol
- 17. Pronombres personales – Simulado Enem de Espanhol com 10 questões
- 18. Questões de interpretação de texto em espanhol
- 19. Regras de Acentuação no Espanhol: resumo com simulado
- 20. Resumo de Espanhol com Simulado de Muy e Mucho
- 21. Verbo gustar – Simulado Enem de Espanhol com 10 questões
Sociologia
- 1. 10 questões sobre gênero e construção social do sexo
- 2. A Sociologia como Ciência: resumo com simulado Enem
- 3. As ideias de Karl Marx: resumo de filosofia com simulado Enem
- 4. Comunidade e Sociedade: aula gratuita com Simulado Enem de Sociologia
- 5. Controle Social – Resumo com Simulado Enem de Sociologia
- 6. Émile Durkheim – Resumo com Simulado Enem de Sociologia
- 7. Exercícios sobre a globalização
- 8. Indústria Cultural: resumo com Simulado Enem de Sociologia
- 9. Lista de exercícios sobre Max Weber: resumo com simulado
- 10. O positivismo de de Auguste Comte: resumo de Sociologia Enem
- 11. O surgimento da Sociologia como ciência: resumo Enem
- 12. Questões do Enem sobre desigualdade de gênero
- 13. Questões sobre cidadania e direitos: resumo Enem
- 14. Questões sobre meio ambiente e sustentabilidade
- 15. Questões sobre movimentos sociais
- 16. Questões sobre racismo e discriminação racial no Brasil
- 17. Questões sobre tecnologia e era informacional: resumo com simulado
- 18. Questões sobre trabalho no mundo atual, na 3ª Revolução Industrial
- 19. Resumo de Grupos Sociais, com Simulado Enem de Sociologia
Encceja
- 1. 10 questões sobre as Leis de Newton
- 2. 10 questões sobre Teorema de Pitágoras e relações do triângulo retângulo
- 3. A Colonização Portuguesa no Brasil – História Enem & Encceja
- 4. A Economia Açucareira do Brasil Colonial: história Enem e Encceja
- 5. A Era Vargas de 1930 a 1945: veja as características do período
- 6. A Evolução das Espécies: resumo de Biologia com Simulado
- 7. A origem da Física como ciência: resumo Enem com Simulado
- 8. A Origem das Espécies e Charles Darwin: Biologia Enem & Encceja
- 9. A Posição Geográfica do Brasil: resumo Enem com Simulado
- 10. A Primeira Lei de Mendel. Resumo com Simulado de Genética
- 11. A Regra de Três; Razão e Proporção: resumo com Simulado
- 12. A República Populista: Período Democrático de 1945 a 1964
- 13. A Revolução Industrial – Resumo com Simulado Enem & Encceja
- 14. A Revolução Industrial e os meios de transporte – Simulado Encceja
- 15. A Segunda Guerra Mundial – Resumo com Simulado
- 16. Absolutismo – Resumo e Simulado de História Enem & Encceja
- 17. Ácidos e Bases: resumo de Química com Simulado
- 18. Ambiente: os Biomas brasileiros e a seleção natural – Resumo com Simulado Encceja
- 19. Ângulos, Probabilidade, e Soma – Simulado Encceja e Enem
- 20. Aquecimento Global e Problemas Ambientais: Geografia Enem & Encceja
- 21. Aquecimento Global: resumo com Simulado Enem & Encceja
- 22. Arte no cotidiano e nas palavras – Simulado Encceja
- 23. Artigos Definidos e Artigos Indefinidos: resumo de Gramática
- 24. As Bacias Hidrográficas: ciclo das águas e formação dos rios
- 25. As Características do Romantismo: resumo Enem & Encceja
- 26. As Funções da Linguagem – Resumo com Simulado de Literatura
- 27. As ideias de Karl Marx: resumo de filosofia com simulado Enem
- 28. As Relações Ecológicas – Resumo Enem & Encceja com Simulado
- 29. As Revoltas Coloniais no Brasil: resumo e simulado de História
- 30. Blocos econômicos, desigualdade social e migração – Simulado Encceja
- 31. Cadeias de Carbono – Resumo com Simulado Enem de Química
- 32. Características Básicas dos Seres Vivos: resumo com simulado
- 33. Civilização da Mesopotâmia: resumo Enem & Encceja com Simulado de História
- 34. Civilização dos Fenícios – Resumo e Simulado de História Enem
- 35. Combustível limpo, genética e reciclagem – Simulado Encceja
- 36. Como será a prova do Encceja 2024?
- 37. Compostos químicos, vírus e calor – Simulado Encceja
- 38. Conjuntos: resumo online com Simulado Enem & Encceja de Matemática
- 39. Construção do território – Simulado Encceja
- 40. Continente Africano: Resumo com Simulado de Geografia Enem
- 41. Controle Social – Resumo com Simulado Enem de Sociologia
- 42. Covid-19, a volta do Sarampo e a crise das vacinas no Brasil
- 43. Critérios de Divisibilidade: resumo com Simulado de Matemática
- 44. Cultura das organizações trabalhistas e Semana de Arte Moderna – Simulado Encceja
- 45. Cultura indígena, cultura afro-brasileira e o Estado Novo – Simulado Encceja
- 46. Cultura, identidade e território – Simulado Encceja
- 47. Curso Intensivo do Encceja: 100% grátis. Inscrições abertas
- 48. Dedução Matemática – Simulado Enem & Encceja
- 49. Defendendo ideias e o uso da língua materna – Simulado Encceja
- 50. Definição e propriedades da matéria – Simulado de Química
- 51. Diâmetro e escala – Simulado Encceja
- 52. Diminuição de custos e modernização – Simulado Encceja
- 53. Divisão de poder, Funai e recursos naturais – Simulado Encceja
- 54. Estado e Direito – Simulado Encceja
- 55. Estrangeirismo e memória cultural na Formação das Palavras
- 56. Evolução tecnológica, democracia e IDH – Simulado Encceja
- 57. Êxodo rural, desmatamento e trabalho infantil – Simulado Encceja
- 58. Expansão Marítima e Grandes Navegações: resumo com Simulado
- 59. Filósofos da Natureza – Resumo com Simulado Enem & Encceja
- 60. Frações e Sequências: resumo Encceja de Matemática com Simulado
- 61. Função de 1º Grau: resumo com exemplos e exercícios
- 62. Função do 1º Grau: resumo com Simulado Enem de Matemática
- 63. Gêneros Literários – Revisão Online com Simulado de Literatura
- 64. Homem, um animal político: veja o pensamento de Aristóteles
- 65. IDH, Cibercultura, e desigualdade: resumo de geografia
- 66. Impacto Ambiental: resumo com simulado de Geografia. Vem!
- 67. Indústria Cultural: resumo com Simulado Enem de Sociologia
- 68. Inscrições para o Encceja estão oficialmente abertas; veja como se inscrever
- 69. Interpretação de Textos e de Tirinhas – Resumo com Simulado
- 70. Interpretação em Inglês e Estatuto da Igualdade Racial – Simulado Encceja
- 71. Jean-Jacques Rousseau e o Iluminismo: resumo de filosofia
- 72. Juros Simples e Juros Compostos: Matemática Enem & Encceja
- 73. Leitura de gráficos e imagens: resumo com Simulado
- 74. Leitura de tabelas e probabilidade – Simulado Encceja
- 75. Linguagem Denotativa x Conotativa: resumo com simulado Enem
- 76. Línguas estrangeiras em nossa sociedade – Simulado Encceja
- 77. Lipídios na Biologia do Enem & do Encceja: resumo com Simulado Online
- 78. Lista de exercícios sobre equações do 1º grau: resumo e simulado
- 79. Lista de exercícios sobre hidrografia para o Enem
- 80. Literatura: veja desde a Carta de Pero Vaz de Caminha e até os dias de hoje
- 81. Lógica e Argumentação – Resumo de Matemática Encceja e Enem com Simulado
- 82. Massa, minerais e velocidade – Simulado Encceja
- 83. Média aritmética e paralelepípedo – Simulado Encceja
- 84. Média Simples e Média Ponderada: Resumo Enem & Encceja
- 85. Meiose – Resumo com Simulado de Biologia Enem & Encceja
- 86. Mercantilismo – Resumo com Simulado Enem de História
- 87. Métodos Contraceptivos e mais 10 Temas de Biologia Enem
- 88. Minorias, construção da sociedade e regionalismo – Simulado Encceja
- 89. Mitocôndria e Energia Celular: resumo Enem & Encceja de Biologia
- 90. Nada se cria, nada se perde, tudo se transforma: a Lei de Lavoisier
- 91. Números negativos – Simulado Encceja
- 92. O Átomo do Carbono – Resumo Enem com simulado de Química
- 93. O Cálculo de Porcentagem: resumo com Simulado de Matemática
- 94. O Mito da Caverna de Platão – Simulado de Filosofia
- 95. O Movimento de Rotação da Terra- Resumo Enem com Simulado
- 96. O que é a Filosofia – aula gratuita com Simulado Enem & Encceja
- 97. O Quinhentismo: resumo com simulado de Literatura Enem
- 98. O Romantismo na literatura brasileira: resumo com simulado
- 99. O Sistema Solar e a ordem dos planetas: resumo com simulado
- 100. O uso do Gerúndio – Resumo simulado Enem gratuito
- 101. Oração Subordinada: simulado Enem com resumo de Português
- 102. Os 4 Fusos Horários no Brasil: resumo de Geografia Enem
- 103. Os Filósofos do Iluminismo e a origem da Revolução Francesa
- 104. Os Filósofos Sofistas – Resumo com Simulado Enem & Encceja
- 105. Os seis Biomas Brasileiros: resumo de Geografia com Simulado Enem
- 106. Padronização estética, copa do mundo e interpretação – Simulado Encceja
- 107. Parnasianismo – Resumo com Simulado de Literatura
- 108. Placas Tectônicas: tsunamis, vulcões e terremotos: resumo Enem
- 109. Platão: o Mundo das Ideias e o Mundo dos Sentidos. Filosofia Enem
- 110. Prefixos e Sufixos – Resumo com Simulado Enem & Encceja de Gramática
- 111. Pronomes retos, oblíquos e demonstrativos: resumo com Simulado
- 112. Provas do Encceja: download grátis com gabarito
- 113. Queda Livre + MRU – Veja resumo com Simulado Enem & Encceja de Física
- 114. Regra de Três e Aresta: resumo com simulado Enem
- 115. Reprodução Assexuada – Resumo de Biologia Enem com Simulado
- 116. Resolução de questões de Circuitos Elétricos: Física Enem
- 117. Resumo com simulado de Acentuação Gráfica: Português Enem
- 118. Resumo com simulado de Regra de Três Simples, e Composta
- 119. Resumo da Revolução Francesa, com Simulado de História
- 120. Resumo de Divisão Silábica com simulado Enem de Português
- 121. Resumo de Física sobre Escalas Termométricas, com simulado
- 122. Resumo de Frações: Matemática com Simulado Enem
- 123. Resumo de Geologia Geral com simulado Enem de Geografia
- 124. Resumo de Hidrosfera, com Simulado de Geografia Enem
- 125. Resumo de Progressão Aritmética, com Simulado Enem
- 126. Resumo de Regra de Três: veja como resolver as questões no Enem e no Encceja
- 127. Resumo e Simulado sobre a filosofia de Aristóteles
- 128. Semana de Arte Moderna: literatura Enem. Resumo e Simulado
- 129. Simulado Encceja: testes rápidos de todas as matérias
- 130. Simulado Enem de Biologia – Os temas que mais caem
- 131. Sólido, Líquido, e Gasoso: resumo de Física Enem & Encceja, com Simulado!
- 132. Soma de Vetores – Resumo Online de Física com Simulado Gratuito
- 133. Substantivos: resumo de Português com simulado
- 134. Sustentabilidade, Lei Seca e gírias – Simulado Encceja
- 135. Tecnologia e Ciências em nosso cotidiano – Resumo e Simulado Encceja
- 136. Temas da Redação do Encceja confirmam Problemática Social
- 137. Terceira Geração Modernista – Resumo de Literatura com Simulado
- 138. Transporte marítimo e poluição nuclear – Simulado Encceja
- 139. Veja o Barroco em Portugal – Resumo com Simulado de Literatura
- 140. Veja o Movimento de Translação da Terra ao redor do Sol
- 141. Veja o que são as Proteínas: resumo de biologia Enem
- 142. Vida cotidiana e os impactos ambientais – Simulado Encceja
- 143. Vírus Ebola – Resumo Enem & Encceja com dicas e simulado online