Triângulo é uma figura que possui 3 ângulos internos, 3 lados, e 3 ângulos externos. A soma dos ângulos internos é sempre 180º. E, a soma dos ângulos externos dá, sempre, 360 graus. Confira a explicação completa e teste seus conhecimentos sobre os tipos de triângulos, as classificações pelos tipos de ângulos e o Teorema de Pitágoras. São temas que sempre caem no Enem. Vem!
Veja um resumo rápido da teoria sobre os diversos tipos, características e propriedades dos Triângulos. Em seguida confira as super vídeoaulas com os professores Sérgio Sarkis e Vinny. Ambos apresentam exercícios resolvidos para você aprender de verdade. No final, responda ao simulado Enem & Encceja sobre triângulos no Enem:
Você já sabe que o triângulo é um polígono de três lados. A soma dos ângulos internos é de 180 graus, e a soma dos ângulos externos é de 360 graus. Os polígonos são figuras fechadas, formadas por segmentos de reta. Essa figura geométrica se caracteriza pelos seguintes elementos: ângulos, vértices, diagonais e lados.
Agora, observe a figura a seguir e leia novamente o texto acima, para você aplicar à imagem de um triângulo o que já aprendeu nesta introdução do resumo sobre o que mais de triângulos no Enem.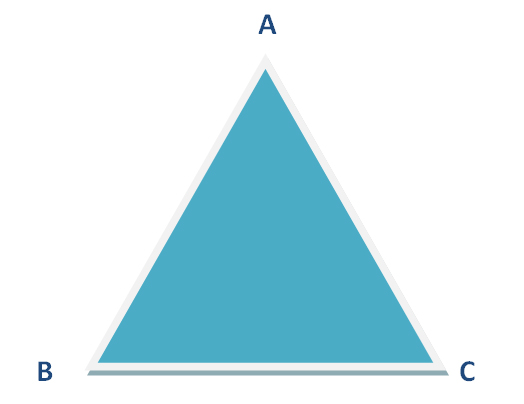 Logo, podemos identificar os seguintes elementos: A, B, C são os vértices dos triângulos. Os lados dos triângulos são simbolizados pelos vértices, que nada mais são do que o ponto de encontro (AB, BC,AC) dos segmentos de retas. Cada lado do triângulo representa um ângulo, logo, tendo três lados, possui três ângulos.
Logo, podemos identificar os seguintes elementos: A, B, C são os vértices dos triângulos. Os lados dos triângulos são simbolizados pelos vértices, que nada mais são do que o ponto de encontro (AB, BC,AC) dos segmentos de retas. Cada lado do triângulo representa um ângulo, logo, tendo três lados, possui três ângulos.
Os tipos de triângulos no Enem
Um triângulo é classificado de acordo com a medida de cada um dos seus lados, ou seja, de cada um dos seus ângulos. Veja abaixo os triângulos Escalenos; Equiláteros; e os Triângulos Isósceles:
Triângulo Escaleno: todos os lados são diferentes.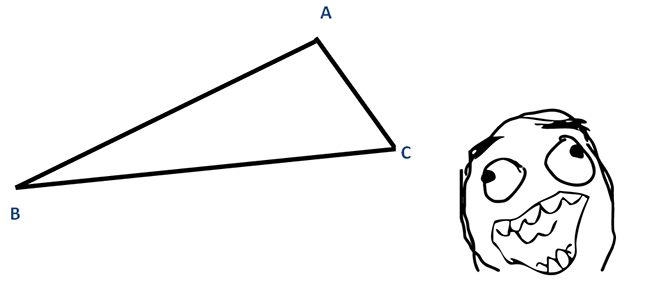 Veja que não há correspondência entre os lados A-B; B-C; e A-C. Todos são diferentes.
Veja que não há correspondência entre os lados A-B; B-C; e A-C. Todos são diferentes.
Triângulo Equilátero: todos os lados e ângulos são iguais. Concluímos que seus ângulos serão de 60°.
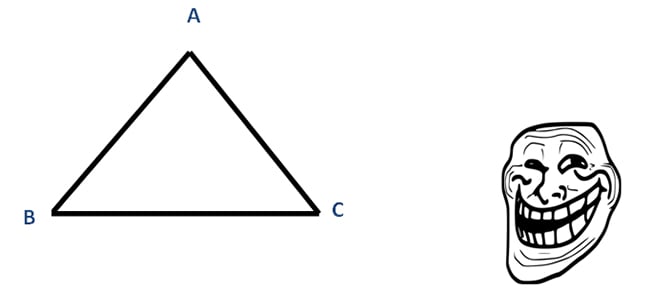 Observe e perceba que A-B = B-C = A-C. Todos os ângulos internos são de 60 graus.
Observe e perceba que A-B = B-C = A-C. Todos os ângulos internos são de 60 graus.
Triângulo Isósceles: Dois lados são iguais – Triângulo isósceles: dois lados iguais, têm a mesma medida, e por isso são chamados de Congruentes. O lado menos é chamado de Base do Triângulo. 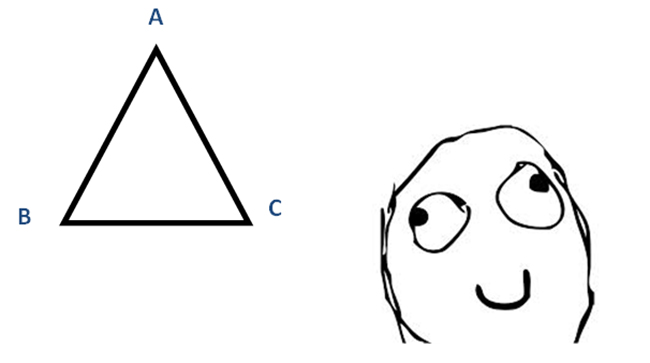 Observe que A-B = A-C; e que B-C é menor do que os Lados Congruentes. Então, B-C forma a Base do Triângulo.
Observe que A-B = A-C; e que B-C é menor do que os Lados Congruentes. Então, B-C forma a Base do Triângulo.
Revise o conteúdo da introdução sobre os triângulos no Enem com esta aula do professor Sérgio Sarkis, do canal do Curso Enem Gratuito:
As dicas do professor Sarkis
- Triângulo é uma figura que possui 3 ângulos e, consequentemente, 3 lados.
- – O triângulo possui 3 ângulos internos e 3 ângulos externos. A soma dos ângulos internos é sempre 180º. Confira a explicação completa e detalhada na lousa, durante o vídeo acima.
- – A soma dos ângulos externos é sempre 360º. Fique ligadinho (a) no detalhamento exposto na lousa também!
- – Outra propriedade importante de decorar é: cada ângulo externo equivale à soma dos ângulos internos não adjacentes. Ficou confuso? Dá o play que o prof te explica!
- – Mais uma propriedade importante: o maior lado do triângulo está sempre diante do maior ângulo. É importante saber disso porque se o triângulo do exercício tiver 3 ângulos diferentes, haverá 3 lados diferentes (escaleno); se houver 3 ângulos iguais, haverá 3 lados iguais (equilátero); se houver 2 ângulos iguais e um diferente, haverá dois lados iguais (isósceles).
- – Confira agora a explicação sobre o teorema da bissetriz interna, que vai te ajudar na resolução de vários exercícios! Lembre-se que bissetriz é a linha que divide o ângulo ao meio.
Triângulo Retângulo e o Teorema de Pitágoras
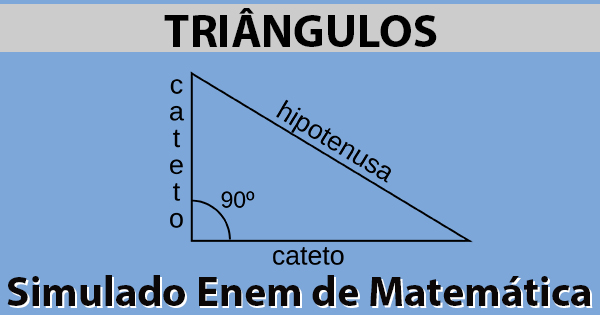
Confira com o professor Sérgio Sarkis, do canal Curso Enem Gratuito, um resumo completo sobre os Triângulos e o Teorema de Pitágoras: a soma do quadrado dos Catetos é igual ao quadrado da Hipotenusa. Veja:
Muito boa esta revisão
Classificações dos Triângulos em relação ao ângulo:
- Os triângulos também podem ser classificados quanto ao ângulo.
- Triângulo Retângulo: tem um ângulo ‘reto’ que mede 90º.
- Triângulo Obtusângulo: tem um ângulo maior que 90°.
- Triângulo Acutângulo: Todos os ângulos são menores de noventa graus.
Triângulos Congruentes
Dois triângulos são denominados congruentes quando possuem a mesma medida nos três lados e nos três ângulos.
Exemplo: Os triângulos ABC e A’B’C’ são congruentes: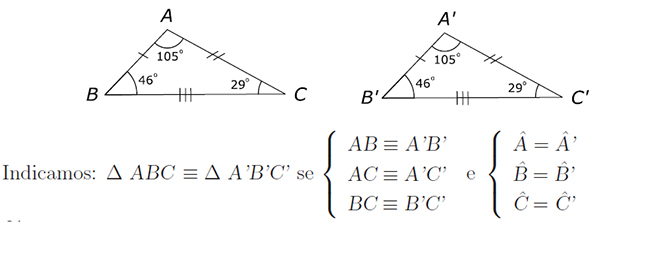
Em dois triângulos congruentes, são congruentes entre si:
a) os lados opostos a ângulos congruentes;
b) os ângulos opostos a lados congruentes;
Existem cinco critérios de congruência entre triângulos. Esse assunto é mais aprofundado no ensino superior, mas ainda assim é cobrado na prova de Matemática do Enem. Mas, o foco principal do seu estudo para o Enem e os Vestibulares deve estar mesmo na semelhança entre os triângulos no Enem.
Cálculos envolvendo Triângulos no Enem
Para mandar bem no Enem, no Encceja e nos vestibulares é importante ir além do Teorema de Pitágoras. Veja nova aula com o professor Sarkis, do Curso Enem Gratuito, com resolução de exercícios sobre Triângulos:
Nota dez esta aula sobre Triângulos. Agora, vamos em frente:
Semelhança entre triângulos
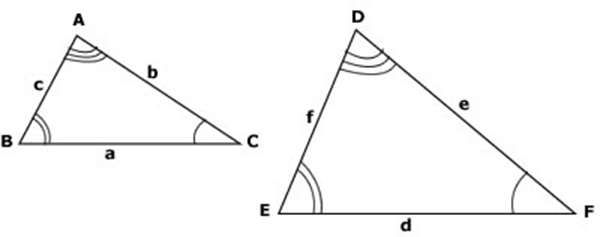
Para descobrir se dois triângulos são semelhantes, você precisa entender o conceito de congruência. Dois triângulos são semelhantes quando seus ângulos são respectivamente congruentes ou os lados correspondentes são proporcionais.
Observação importante: Trata-se de conceito de proporcionalidade – Razão e Proporção.
Razão de semelhança – A razão de semelhança de dois triângulos é uma medida de proporcionalidade entre eles e é dada por uma constante : D/A = E/B = F/C = k.
Para fixar o tema, assista à esta videoaula com o professor Vinny, do Blog do Enem:
Resolução de Exercício de Triângulos no Enem
Para entender e dominar todos esses conceitos, nada melhor do que praticar não é mesmo? Acompanhe a resolução do exercício a seguir.
1) Considerando os triângulos MNP e PQR da figura abaixo, podemos afirmar que ∆MNP ~ ∆PQR. Como você justifica essa afirmação?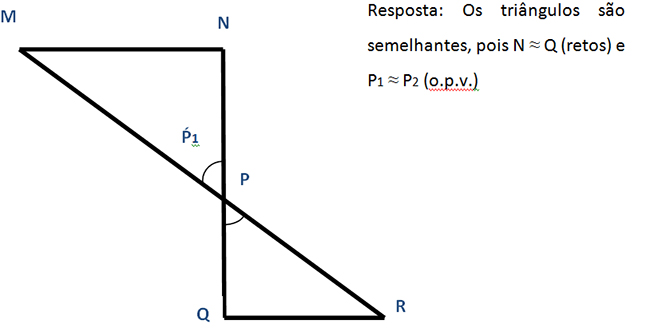
2) Considerando a figura na qual C≈ F e B≈E, determine as medidas x e y nela indicadas.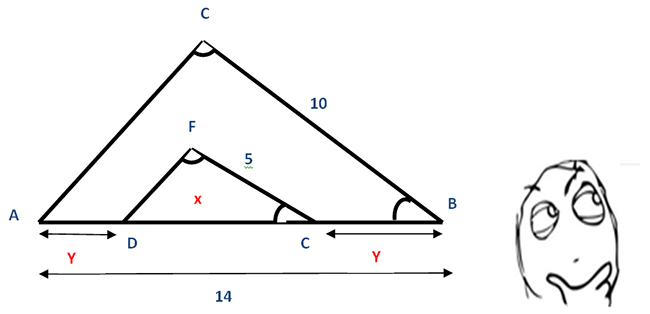
Resolução:
∆ DFE ≈ ∆ ACB
AB = AC = CB → 14 = 10 → 70 = 10x → x =7
DE DF FE x 5
x=7, logo, y = 14-x, logo:
y = 14 – x
y = 7
2
Resposta = Então x=7 e y = 3,5
Agora vem o Simulado!!
Então, aproveite para responder as 10 questões que selecionamos para você sobre os triângulos no Enem, e garanta um bom desempenho na prova de Matemática!
Triângulos no Enem
.
Escolha mais um Simulado Enem para fazer agora
Mandar bem no Enem é tudo de bom. Agora faça mais um Simulado Enem para testar seus conhecimentos e ver as aulas de revisão das questões que você errar. Escolha na tabela no final do post a matéria que você quer revisar agora. Com os testes do Simulado você corrige as suas falhas e aumenta suas chances no próximo Exame Nacional do Ensino Médio.
Venha para o Curso Enem Gratuito:
Criamos para você duas novidades: Um Curso Enem Online totalmente gratuito, e uma bateria de Simulados Enem Gratuitos, com todas as matérias do Exame Nacional do Ensino Médio. Acesse o Curso e faça os Simulados para chegar bem no próximo Enem! Simulados com Gabarito na mesma hora. Veja aqui:
Simulado Enem Online – Escolha a sua próxima prova:
Biologia
- 1. 10 questões sobre vitaminas: simulado de Biologia
- 2. A Evolução das Espécies: resumo de Biologia com Simulado
- 3. A Primeira Lei de Mendel. Resumo com Simulado de Genética
- 4. As funções da Água no Corpo Humano: resumo e simulado
- 5. As Relações Ecológicas – Resumo Enem & Encceja com Simulado
- 6. Características Básicas dos Seres Vivos: resumo com simulado
- 7. Carboidratos – Resumo Enem com Simulado Online de Biologia
- 8. Covid-19, a volta do Sarampo e a crise das vacinas no Brasil
- 9. Cromatina, cromossomos e cariótipo: resumo de Biologia Enem
- 10. Divisão Celular – Resumo de Meiose & Mitose com Simulado
- 11. Enzimas: Resumo com Simulado de Biologia Enem & Encceja
- 12. Exercícios sobre Darwinismo e Lamarckismo
- 13. Exercícios sobre fermentação alcoólica e láctica
- 14. Exercícios sobre membrana plasmática e transportes passivo e ativo
- 15. Intérfase – Resumo de Biologia Enem com Simulado
- 16. Lipídios na Biologia do Enem & do Encceja: resumo com Simulado Online
- 17. Lista de exercícios sobre DNA e RNA – Biologia Enem
- 18. Lista de exercícios sobre genética, com resumo de revisão
- 19. Lista de exercícios sobre respiração celular
- 20. Meiose – Resumo com Simulado de Biologia Enem & Encceja
- 21. Métodos Científicos x Senso Comum: resumo com Simulado Enem
- 22. Métodos Contraceptivos e mais 10 Temas de Biologia Enem
- 23. Métodos Contraceptivos: resumo e simulado Enem de biologia
- 24. Mitocôndria e Energia Celular: resumo Enem & Encceja de Biologia
- 25. Mitose – Revisão e Simulado Enem de Biologia com 10 questões
- 26. O que são os Cromossomos: resumo sobre DNA & RNA
- 27. Os seis Biomas Brasileiros: resumo de Geografia com Simulado Enem
- 28. Os tipos de Microscópios: resumo Enem com simulado
- 29. Questões do Enem sobre a Malária e doenças virais
- 30. Questões sobre evolução das espécies
- 31. Questões sobre organelas celulares
- 32. Questões sobre proteínas a aminoácidos com resumo de Biologia
- 33. Reprodução Assexuada – Resumo de Biologia Enem com Simulado
- 34. Resumo com lista de exercícios sobre Relações Ecológicas
- 35. Sais Minerais: resumo de Biologia Enem com Simulado
- 36. Simulado Enem de Biologia – Os temas que mais caem
- 37. Simulado grátis de Matemática Enem com nota pela TRI
- 38. Sucessão Ecológica – Simulado Enem com aula de revisão gratuita. Veja!
- 39. Teorias sobre a Origem da Vida: resumo com Simulado Enem
- 40. Veja o que são as Proteínas: resumo de biologia Enem
- 41. Veja o Transporte Passivo da Osmose na Membrana Plasmática
- 42. Vírus Ebola – Resumo Enem & Encceja com dicas e simulado online
- 43. Zika Vírus e Microcefalia: resumo de Biologia com simulado
Filosofia
- 1. Exercícios sobre Escola de Frankfurt
- 2. Exercícios sobre os filósofos da natureza
- 3. Filósofos da Natureza – Resumo com Simulado Enem & Encceja
- 4. Homem, um animal político: veja o pensamento de Aristóteles
- 5. Indústria Cultural: resumo com Simulado Enem de Sociologia
- 6. Jean-Jacques Rousseau e o Iluminismo: resumo de filosofia
- 7. Lista de questões sobre Immanuel Kant
- 8. O Mito da Caverna de Platão – Simulado de Filosofia
- 9. O Pensamento Mítico – Resumo de Filosofia Enem com Simulado
- 10. O que é a Filosofia – aula gratuita com Simulado Enem & Encceja
- 11. O que são os Mitos – Resumo com Simulado Enem de Filosofia
- 12. Os Filósofos do Iluminismo e a origem da Revolução Francesa
- 13. Os Filósofos Sofistas – Resumo com Simulado Enem & Encceja
- 14. Platão e as formas de governo: resumo com Simulado Enem
- 15. Platão e as ideias de justiça e política: resumo com exercícios
- 16. Platão e o Mundo das Ideias: resumo de Filosofia com simulado
- 17. Questões sobre ética
- 18. Questões sobre existencialismo
- 19. Questões sobre Nicolau Maquiavel. Resumo com simulado
- 20. Questões sobre René Descartes e o Racionalismo
- 21. Questões sobre Rousseau: o Iluminismo e a Revolução Francesa
- 22. Questões sobre Thomas Hobbes
- 23. Resumo e Simulado sobre a filosofia de Aristóteles
- 24. Sócrates e o Oráculo de Delfos: resumo de Filosofia Enem
- 25. Sócrates e o Pensamento Sofista: resumo Enem de Filosofia
- 26. Veja os Filósofos da Natureza – Resumo de Filosofia Enem
Física
- 1. 10 questões sobre as Leis de Newton
- 2. A origem da Física como ciência: resumo Enem com Simulado
- 3. A primeira lei da termodinâmica: resumo com simulado de Física
- 4. Acústica: lista de exercícios do Enem e vestibulares
- 5. Definição e Soma de Vetores: veja resumo com Simulado Enem
- 6. Equilíbrio de Corpo Extenso – Simulado de Física
- 7. Exercícios sobre energia cinética: velocidade e aceleração
- 8. Exercícios sobre fenômenos ondulatórios
- 9. Exercícios sobre óptica geométrica
- 10. Exercícios sobre transmissão de calor
- 11. Força Atrito – Simulado Enem Online de Física com 10 questões
- 12. Grandezas vetoriais e escalares: resumo de Física com simulado
- 13. Hidrostática: resumo online de Física com Simulado Enem
- 14. Impulso e Quantidade de Movimento – Simulado de Física Enem
- 15. Lançamento de Peso – Simulado Enem Online de Física com 10 questões
- 16. Lista de exercícios sobre as 3 Leis de Newton
- 17. Lista de exercícios sobre calorimetria, com resumo de física
- 18. Lista de exercícios sobre ondulatória
- 19. Lista de exercícios sobre potência elétrica
- 20. Movimento Circular Uniforme: resumo com Simulado de Física
- 21. Movimento Retilíneo Uniforme + MRUV: resumo com simulado
- 22. MRU + MRUV: resumo online com Simulado Enem de Física
- 23. O Princípio de Arquimedes: resumo de Física com Simulado
- 24. Óptica – Resumo com Simulado Enem de Física
- 25. Queda Livre + MRU – Veja resumo com Simulado Enem & Encceja de Física
- 26. Repouso e Movimento: aprenda Física com resumo e simulado
- 27. Resolução de questões de Circuitos Elétricos: Física Enem
- 28. Resumo com lista de exercícios sobre Movimento Uniforme
- 29. Resumo da 1ª Lei da Termodinâmica, com Simulado Enem de Física
- 30. Resumo de Física sobre Escalas Termométricas, com simulado
- 31. Simulado de Física Básica do Enem – Teste seu nível em 10 questões
- 32. Sistema Internacional de Unidades (SIU) – Simulado Enem
- 33. Sistemas conservativos – Simulado de Física com 10 questões
- 34. Soma de Vetores – Resumo Online de Física com Simulado Gratuito
- 35. Transmissão de Calor – Simulado Enem Online de Física com 10 questões
- 36. Velocidade – Simulado Enem Online de Física com 10 questões
- 37. Velocidade, Aceleração, Tempo e Espaço. Simulado de Física – Cinemática
Geografia
- 1. 10 vezes que a Ucrânia caiu no Enem e vestibulares
- 2. A Deriva Continental e o movimento das Placas Tectônicas
- 3. A Divisão Política do Brasil: resumo com simulado de Geografia
- 4. A história geológica da Terra: resumo com simulado Enem
- 5. A Posição Geográfica do Brasil: resumo Enem com Simulado
- 6. A Rosa dos Ventos e os 4 Pontos Cardeais: resumo com simulado
- 7. Aquecimento Global: resumo com Simulado Enem & Encceja
- 8. As Camadas da Atmosfera: resumo & simulado de geografia Enem
- 9. As Eras Geológicas – Resumo Online com Simulado Enem de Geografia
- 10. Características do Continente Europeu: resumo e simulado Enem
- 11. Comércio Exterior – Simulado Enem Online de Geografia com 10 questões
- 12. Continente Africano: Resumo com Simulado de Geografia Enem
- 13. Crosta terrestre ou litosfera: resumo com imulado de Geografia
- 14. Escala Cartográfica – Resumo enem de Geografia com Simulado
- 15. Espaço rural brasileiro – Resumo de Geografia Enem com Simulado
- 16. Exercícios sobre as fontes de energia e a matriz energética no Brasil
- 17. Exercícios sobre degradação ambiental
- 18. Exercícios sobre formação e degradação do solo
- 19. Fusos Horários no Brasil – Resumo com Simulado Enem de Geografia
- 20. GPS – Resumo com Simulado Enem de Geografia
- 21. Impacto Ambiental: resumo com simulado de Geografia. Vem!
- 22. Latitude e Longitude: resumo com simulado de Geografia
- 23. Lista de exercícios sobre a indústria brasileira
- 24. Lista de exercícios sobre globalização
- 25. Lista de exercícios sobre hidrografia para o Enem
- 26. Lista de exercícios sobre urbanização brasileira
- 27. Lista de questões sobre a Otan
- 28. Lista de questões sobre cartografia
- 29. O Movimento de Rotação da Terra- Resumo Enem com Simulado
- 30. O Sistema Solar e a ordem dos planetas: resumo com simulado
- 31. Origem do Universo – Simulado Enem de Geografia com 10 questões
- 32. Placas Tectônicas: tsunamis, vulcões e terremotos: resumo Enem
- 33. Projeções cartográficas cilíndricas: resumo com simulado Enem
- 34. Questões sobre clima e climatologia
- 35. Recursos minerais – Simulado Enem Online de Geografia com 10 questões
- 36. Resumo com Simulado de Geografia: os 10 temas que mais caem
- 37. Resumo de Geologia Geral com simulado Enem de Geografia
- 38. Resumo de Hidrosfera, com Simulado de Geografia Enem
- 39. Tipos de rochas – Simulado Enem de Geografia com 10 questões
- 40. Veja o Movimento de Translação da Terra ao redor do Sol
Gramática
- 1. 10 questões sobre coesão textual na redação do Enem
- 2. 10 questões sobre Figuras de Linguagem
- 3. 10 questões sobre formação de palavras
- 4. A Função do Advérbio: resumo com simulado de Gramática
- 5. A Morfologia das Palavras no Português: resumo Enem
- 6. Adjetivos – Resumo com Simulado Enem de Português
- 7. Artigos Definidos e Artigos Indefinidos: resumo de Gramática
- 8. As sílabas tônicas: resumo de Gramática com simulado
- 9. Cognatos, homônimos e parônimos – Revisão e Simulado Enem de Gramática
- 10. Conjunções Adverbiais – Resumo com Simulado Enem de Gramática. Veja!
- 11. Exercícios sobre os usos da vírgula
- 12. Exercícios sobre termos acessórios da oração: adjuntos, aposto e vocativo
- 13. Interpretação de Textos e de Tirinhas – Resumo com Simulado
- 14. Lista de exercícios sobre acentuação gráfica
- 15. Lista de exercícios sobre conotação e denotação
- 16. Lista de exercícios sobre formação de palavras
- 17. Lista de exercícios sobre prefixo e sufixo
- 18. Modo indicativo: resumo de português com simulado Enem
- 19. Modo Verbal (Subjuntivo e Imperativo): resumo e simulado de gramática
- 20. O uso do Gerúndio – Resumo simulado Enem gratuito
- 21. Oração Subordinada: simulado Enem com resumo de Português
- 22. Ortografia: o uso das letras – Simulado Enem Online de Gramática com 10 questões
- 23. Os 5 Tipos de Sujeito – Resumo e simulado Enem de Português
- 24. Prefixos e Sufixos – Resumo com Simulado Enem & Encceja de Gramática
- 25. Pronomes e elementos de coesão – Simulado Enem de Gramática
- 26. Pronomes retos, oblíquos e demonstrativos: resumo com Simulado
- 27. Questões de interpretação de texto: dicas de português Enerm
- 28. Recursos Ortográficos e Efeitos de Sentido: resumo com simulado
- 29. Resumo com exercícios sobre linguagem verbal e não verbal
- 30. Resumo com lista de exercícios sobre as funções da linguagem
- 31. Resumo com simulado de Acentuação Gráfica: Português Enem
- 32. Resumo de Acentuação Gráfica com Simulado Enem de Gramática
- 33. Resumo de Divisão Silábica com simulado Enem de Português
- 34. Resumo de Fonemas, com simulado de Português Enem
- 35. Sinais de Pontuação: veja aula gratuita com Simulado Enem de Gramática
- 36. Substantivos: resumo de Português com simulado
- 37. Variedades Linguísticas: resumo de Gramática com simulado
- 38. Veja 10 dicas de Gramática com Simulado Enem
- 39. Veja a Oração Reduzida no resumo Enem de Português
- 40. Veja os Sinônimos e os Antônimos: resumo Enem de Gramática
História
- 1. A Ditadura Militar no Brasil: resumo e simulado Enem de História
- 2. A Era Vargas de 1930 a 1945: veja as características do período
- 3. A Ideologia Nazista – Resumo com simulado de História Enem
- 4. A República Populista: Período Democrático de 1945 a 1964
- 5. A Revolução Industrial – Resumo com Simulado Enem & Encceja
- 6. A Segunda Guerra Mundial – Resumo com Simulado
- 7. Absolutismo – Resumo e Simulado de História Enem & Encceja
- 8. Antiguidade Clássica: resumo e simulado de História Enem
- 9. As Revoltas Coloniais no Brasil: resumo e simulado de História
- 10. Ciclo do café no Brasil: resumo e questões
- 11. Civilização Árabe – Resumo com Simulado Enem de História
- 12. Civilização da Mesopotâmia: resumo Enem & Encceja com Simulado de História
- 13. Civilização dos Fenícios – Resumo e Simulado de História Enem
- 14. Civilização Romana – Resumo Enem com aula gratuita e Simulado
- 15. Exercícios sobre a colonização mercantilista europeia
- 16. Exercícios sobre a sociedade colonial no Brasil
- 17. Exercícios sobre Baixa Idade Média
- 18. Exercícios sobre renascimento comercial e urbano
- 19. Exercícios sobre revoltas coloniais nativistas
- 20. Expansão Marítima e Grandes Navegações: resumo com Simulado
- 21. Grécia Antiga: lista de exercícios e resumo
- 22. História das eleições no Brasil – Resumo e questões
- 23. Império Bizantino – Simulado Enem Online de História com 10 questões
- 24. Lista de exercícios sobre a Revolução Francesa
- 25. Lista de exercícios sobre o Segundo Reinado
- 26. Mercantilismo – Resumo com Simulado Enem de História
- 27. Nova República – Simulado Enem Online de História com 10 questões
- 28. O Egito Antigo e as pirâmides dos Faraós: resumo de História
- 29. O Fascismo italiano – Resumo de HIstória com Simulado Enem
- 30. Os Hebreus – Resumo com simulado: a História dos Judeus
- 31. Os Persas: resumo com Simulado Enem de História
- 32. Pré História – Aula gratuita com Simulado Enem Online
- 33. Questões sobre a independência do Brasil
- 34. Questões sobre a vinda da família real para o Brasil
- 35. Questões sobre o ciclo da cana-de-açúcar Brasil colonial
- 36. República Velha: Aula gratuita e simulado de História
- 37. Resumo com Simulado Enem: o ciclo das Grandes Navegações
- 38. Resumo da Escravidão, Resistência, Abolição e Racismo no Brasil
- 39. Resumo da Revolução Francesa, com Simulado de História
- 40. Resumo de História e Filosofia Enem com Simulado de Iluminismo
- 41. Resumo Enem de Pré-História com dicas e Simulado
- 42. Teorias da História – Simulado Enem Online de História com 10 questões
Inglês
- 1. Adjetivos em Inglês e Interpretação de textos no Enem
- 2. Advérbios de frequência – Simulado Enem de Inglês com 10 questões
- 3. Apóstrofo – Revisão e Simulado Enem de Inglês com 10 questões
- 4. Artigo Definido – Simulado Enem Online de Inglês com 10 questões
- 5. Artigos Indefinidos: resumo com simulado de Inglês
- 6. Como interpretar textos em Inglês: resumo com simulado Enem
- 7. Conditionals – Simulado Enem de Inglês com 10 questões
- 8. Exercícios sobre verbos regulares e irregulares
- 9. Inglês no Enem: dicas sobre os Nouns. Resumo com Simulado
- 10. Interpretação de texto em inglês: veja as técnicas de Skimming e Scanning
- 11. Interrogative Pronouns: resumo com simulado Enem de Inglês
- 12. Nominal Groups – Simulado Enem Online de Inglês com 10 questões
- 13. Prepositions – Resumo com Simulado Enem de Inglês
- 14. Present Continuous no Inglês: resumo com simulado Enem
- 15. Present Perfect no Inglês: resumo com simulado Enem
- 16. Pronomes em Inglês: veja no resumo com simulado Enem
- 17. Pronomes Indefinidos – Simulado Enem de Inglês com 10 questões
- 18. Pronomes Relativos em Inglês: veja no resumo com simulado
- 19. Quantificadores – Resumo com simulado de Inglês Enem
- 20. Question Words: veja um resumo com simulado Enem de Inglês
- 21. Questões sobre interpretação de músicas e poemas em inglês
- 22. Questões sobre interpretação de texto em inglês com gabarito
- 23. Simple Present – Aula gratuita com Simulado Enem
- 24. Singular e Plural – Resumo de Inglês com dicas e simulado
- 25. Substantivos Contáveis e Incontáveis – Simulado Enem de Inglês
- 26. Veja o verbo To Be: resumo com simulado Enem de Inglês
Literatura
- 1. As Características do Romantismo: resumo Enem & Encceja
- 2. As funções da Arte Literária: resumo Enem com Simulado Online
- 3. As Funções da Linguagem – Resumo com Simulado de Literatura
- 4. Classicismo – Resumo com Simulado de Literatura Enem & Encceja
- 5. Exercícios sobre Clarice Lispector, com resumo de literatura
- 6. Exercícios sobre o Simbolismo no Brasil
- 7. Gênero Dramático – Resumo com Simulado Enem de Literatura
- 8. Gêneros Literários – Revisão Online com Simulado de Literatura
- 9. Intertextualidade: Resumo de Literatura Enem com Simulado
- 10. Linguagem Denotativa x Conotativa: resumo com simulado Enem
- 11. Lista de exercícios sobre figuras de linguagem
- 12. Lista de exercícios sobre o Realismo no Brasil
- 13. Naturalismo – Resumo de Literatura Enem com Simulado
- 14. O Arcadismo na literatura do Enem: resumo com Simulado
- 15. O que é Metalinguagem: veja no resumo Enem de Literatura
- 16. O Quinhentismo: resumo com simulado de Literatura Enem
- 17. O Romantismo e a Poesia pela Liberdade e contra a Escravidão
- 18. O Romantismo na literatura brasileira: resumo com simulado
- 19. Os Tipos Textuais: resumo sobre o estilo da Redação Enem
- 20. Parnasianismo – Resumo com Simulado de Literatura
- 21. Questões sobre a primeira fase do Modernismo no Brasil
- 22. Questões sobre a Segunda Fase do Modernismo
- 23. Questões sobre música no Enem e vestibulares
- 24. Questões sobre Pré-Modernismo – Exercícios de Literatura
- 25. Questões sobre terceira fase do Modernismo
- 26. Resumo com exercícios sobre o Romantismo no Brasil
- 27. Resumo das Vanguardas Europeias, com simulado Enem
- 28. Resumo e lista de exercícios sobre Machado de Assis
- 29. Resumo sobre Função Poética da Linguagem: literatura Enem
- 30. Revisão – Simulado Enem Online de Literatura com 10 questões
- 31. Segunda fase do Modernismo no Brasil
- 32. Semana de Arte Moderna: literatura Enem. Resumo e Simulado
- 33. Terceira Geração Modernista – Resumo de Literatura com Simulado
- 34. Veja o Barroco em Portugal – Resumo com Simulado de Literatura
- 35. Veja o Barroco no Brasil: resumo com simulado de Literatura
Matemática
- 1. 10 questões sobre cálculo de juros simples e compostos
- 2. 10 questões sobre porcentagem: resumo com simulado
- 3. 10 questões sobre Teorema de Pitágoras e relações do triângulo retângulo
- 4. Binômio de Newton – Resumo Online com Simulado Enem Gratuito
- 5. Circunferência trigonométrica: resumo e simulado Enem
- 6. Conjuntos: resumo online com Simulado Enem & Encceja de Matemática
- 7. Critérios de Divisibilidade: resumo com Simulado de Matemática
- 8. Dedução Matemática – Simulado Enem & Encceja
- 9. Dominando a Matemática para o Enem: Aulão Especial e Simulado com Nota pela TRI
- 10. Exercícios sobre análise combinatória e Princípio Fundamental da Contagem
- 11. Exercícios sobre equação de 2º grau e fórmula de Bhaskara
- 12. Exercícios sobre figuras planas
- 13. Exercícios sobre triângulo retângulo e o Teorema de Pitágoras
- 14. Expressões algébricas – Resumo Enem de Matemática com Simulado
- 15. Função de 1º Grau: resumo com exemplos e exercícios
- 16. Função de Primeiro Grau – Resumo com Simulado Enem
- 17. Função do 1º Grau: resumo com Simulado Enem de Matemática
- 18. Juros Simples e Juros Compostos: Matemática Enem & Encceja
- 19. Leitura de gráficos e imagens: resumo com Simulado
- 20. Lista de exercícios sobre equações do 1º grau: resumo e simulado
- 21. Lista de exercícios sobre média aritmética simples e ponderada
- 22. Lista de exercícios sobre regra de três
- 23. Lista de exercícios sobre sistemas lineares: matemática Enem
- 24. Matemática no Enem: professor ensina como resolver as questões da prova
- 25. Média Simples e Média Ponderada: Resumo Enem & Encceja
- 26. O Ângulo e suas classificações: resumo com Simulado Enem
- 27. O Cálculo de Porcentagem: resumo com Simulado de Matemática
- 28. Os Números Complexos: resumo com Simulado Enem de Matemática
- 29. Potência de base 10 – Resumo e simulado Enem de Matemática
- 30. Potenciação – Resumo com Simulado Enem de Matemática
- 31. Probabilidade – Resumo de Matemática com Simulado Enem & Encceja
- 32. Regra de Três e Aresta: resumo com simulado Enem
- 33. Resumo com Lista de Exercícios sobre polinômios
- 34. Resumo com Lista de Exercícios sobre porcentagem
- 35. Resumo com simulado de Regra de Três Simples, e Composta
- 36. Resumo de Frações: Matemática com Simulado Enem
- 37. Resumo de Progressão Aritmética, com Simulado Enem
- 38. Resumo e exercícios sobre razão e proporção
- 39. Simulado de Notação Científica, com resumo de Matemática
- 40. Simulado grátis de Matemática Enem com nota pela TRI
- 41. Triângulos no Enem: veja o resumo com simulado gratuito
Química
- 1. A Configuração dos Elétrons: resumo Enem de Química
- 2. Ácidos e Bases: resumo de Química com Simulado
- 3. Cadeias de Carbono – Resumo com Simulado Enem de Química
- 4. Cálculo Estequiométrico – Resumo com Simulado Enem de Química
- 5. Cinética química – Simulado Enem de Química
- 6. Definição e propriedades da matéria – Simulado de Química
- 7. Diluição de Soluções – Simulado Enem Online de Química com 10 questões
- 8. Exercícios sobre concentração comum e molar de soluções
- 9. Exercícios sobre ligações químicas iônicas e covalentes
- 10. Exercícios sobre radioatividade
- 11. Exercícios sobre tabela periódica com resumo de Química
- 12. Fatores que alteram a cinética química – Simulado Enem
- 13. Fórmula Empírica e Molecular: resumo e simulado Enem
- 14. Lista de exercícios sobre compostos orgânicos
- 15. Lista de exercícios sobre eletroquímica, com resumo grátis
- 16. Lista de exercícios sobre forças intermoleculares
- 17. Modelos Atômicos – Simulado Enem com aula gratuita
- 18. Mol e Número de Avogadro: resumo com simulado
- 19. Nada se cria, nada se perde, tudo se transforma: a Lei de Lavoisier
- 20. O Átomo do Carbono – Resumo Enem com simulado de Química
- 21. O Diagrama de Fases: resumo Enem de Química com simulado
- 22. O que é fórmula molecular, fórmula empírica e fórmula mínima
- 23. Radioatividade no Enem: resumo com simullado de Química
- 24. Resumo com exercícios sobre estrutura atômica
- 25. Resumo com Exercícios sobre Química Ambiental no Enem
- 26. Resumo com Simulado Enem de Química: teste seu nível
- 27. Resumo de Química com exercícios de funções orgânicas
- 28. Simulado de Equilíbrio Químico: veja o resumo antes de responder
- 29. Sólido; Líquido; e Gasoso: os Estados físicos da matéria
- 30. Soluções Químicas no Enem: Soluto; Solvente; e Solubilidade
- 31. Tabela Periódica: resumo com simulado de Química Enem e Encceja
Espanhol
- 1. Acentuação no Espanhol – Resumo com Simulado Enem
- 2. Adjetivos – Revisão e Simulado Enem de Espanhol com 10 questões
- 3. Artículo neutro – Revisão e Simulado Enem de Espanhol com 10 questões
- 4. Artículos e Contracciones – Simulado Enem Online de Espanhol
- 5. Conjunções Subordinada. Resumo de Espanhol Enem
- 6. Gênero e número dos substantivos – Simulado Enem de Espanhol
- 7. Heterogenéricos – Simulado Enem de Espanhol com 10 questões
- 8. Heterotônicos – Resumo com Simulado Enem de Espanhol
- 9. Los demonstrativos – Simulado Enem Online de Espanhol com 10 questões
- 10. Los numerales cardinales y las horas: Simulado de Espanhol
- 11. Los posesivos – Simulado Enem Online de Espanhol com 10 questões
- 12. Números Ordinais – Simulado Enem Online de Espanhol com 10 questões
- 13. Os porquês – Resumo com Simulado Enem de Espanhol
- 14. Plural – Simulado Enem de Espanhol com 10 questões
- 15. Presente do Indicativo. Resumo com simulado Enem de Espanhol
- 16. Pronombres Interrogativos: resumo com simulado de Espanhol
- 17. Pronombres personales – Simulado Enem de Espanhol com 10 questões
- 18. Questões de interpretação de texto em espanhol
- 19. Regras de Acentuação no Espanhol: resumo com simulado
- 20. Resumo de Espanhol com Simulado de Muy e Mucho
- 21. Verbo gustar – Simulado Enem de Espanhol com 10 questões
Sociologia
- 1. 10 questões sobre gênero e construção social do sexo
- 2. A Sociologia como Ciência: resumo com simulado Enem
- 3. As ideias de Karl Marx: resumo de filosofia com simulado Enem
- 4. Comunidade e Sociedade: aula gratuita com Simulado Enem de Sociologia
- 5. Controle Social – Resumo com Simulado Enem de Sociologia
- 6. Émile Durkheim – Resumo com Simulado Enem de Sociologia
- 7. Exercícios sobre a globalização
- 8. Indústria Cultural: resumo com Simulado Enem de Sociologia
- 9. Lista de exercícios sobre Max Weber: resumo com simulado
- 10. O positivismo de de Auguste Comte: resumo de Sociologia Enem
- 11. O surgimento da Sociologia como ciência: resumo Enem
- 12. Questões do Enem sobre desigualdade de gênero
- 13. Questões sobre cidadania e direitos: resumo Enem
- 14. Questões sobre meio ambiente e sustentabilidade
- 15. Questões sobre movimentos sociais
- 16. Questões sobre racismo e discriminação racial no Brasil
- 17. Questões sobre tecnologia e era informacional: resumo com simulado
- 18. Questões sobre trabalho no mundo atual, na 3ª Revolução Industrial
- 19. Resumo de Grupos Sociais, com Simulado Enem de Sociologia
Encceja
- 1. 10 questões sobre as Leis de Newton
- 2. 10 questões sobre Teorema de Pitágoras e relações do triângulo retângulo
- 3. A Colonização Portuguesa no Brasil – História Enem & Encceja
- 4. A Economia Açucareira do Brasil Colonial: história Enem e Encceja
- 5. A Era Vargas de 1930 a 1945: veja as características do período
- 6. A Evolução das Espécies: resumo de Biologia com Simulado
- 7. A origem da Física como ciência: resumo Enem com Simulado
- 8. A Origem das Espécies e Charles Darwin: Biologia Enem & Encceja
- 9. A Posição Geográfica do Brasil: resumo Enem com Simulado
- 10. A Primeira Lei de Mendel. Resumo com Simulado de Genética
- 11. A Regra de Três; Razão e Proporção: resumo com Simulado
- 12. A República Populista: Período Democrático de 1945 a 1964
- 13. A Revolução Industrial – Resumo com Simulado Enem & Encceja
- 14. A Revolução Industrial e os meios de transporte – Simulado Encceja
- 15. A Segunda Guerra Mundial – Resumo com Simulado
- 16. Absolutismo – Resumo e Simulado de História Enem & Encceja
- 17. Ácidos e Bases: resumo de Química com Simulado
- 18. Ambiente: os Biomas brasileiros e a seleção natural – Resumo com Simulado Encceja
- 19. Ângulos, Probabilidade, e Soma – Simulado Encceja e Enem
- 20. Aquecimento Global e Problemas Ambientais: Geografia Enem & Encceja
- 21. Aquecimento Global: resumo com Simulado Enem & Encceja
- 22. Arte no cotidiano e nas palavras – Simulado Encceja
- 23. Artigos Definidos e Artigos Indefinidos: resumo de Gramática
- 24. As Bacias Hidrográficas: ciclo das águas e formação dos rios
- 25. As Características do Romantismo: resumo Enem & Encceja
- 26. As Funções da Linguagem – Resumo com Simulado de Literatura
- 27. As ideias de Karl Marx: resumo de filosofia com simulado Enem
- 28. As Relações Ecológicas – Resumo Enem & Encceja com Simulado
- 29. As Revoltas Coloniais no Brasil: resumo e simulado de História
- 30. Blocos econômicos, desigualdade social e migração – Simulado Encceja
- 31. Cadeias de Carbono – Resumo com Simulado Enem de Química
- 32. Características Básicas dos Seres Vivos: resumo com simulado
- 33. Civilização da Mesopotâmia: resumo Enem & Encceja com Simulado de História
- 34. Civilização dos Fenícios – Resumo e Simulado de História Enem
- 35. Combustível limpo, genética e reciclagem – Simulado Encceja
- 36. Como será a prova do Encceja 2024?
- 37. Compostos químicos, vírus e calor – Simulado Encceja
- 38. Conjuntos: resumo online com Simulado Enem & Encceja de Matemática
- 39. Construção do território – Simulado Encceja
- 40. Continente Africano: Resumo com Simulado de Geografia Enem
- 41. Controle Social – Resumo com Simulado Enem de Sociologia
- 42. Covid-19, a volta do Sarampo e a crise das vacinas no Brasil
- 43. Critérios de Divisibilidade: resumo com Simulado de Matemática
- 44. Cultura das organizações trabalhistas e Semana de Arte Moderna – Simulado Encceja
- 45. Cultura indígena, cultura afro-brasileira e o Estado Novo – Simulado Encceja
- 46. Cultura, identidade e território – Simulado Encceja
- 47. Curso Intensivo do Encceja: 100% grátis. Inscrições abertas
- 48. Dedução Matemática – Simulado Enem & Encceja
- 49. Defendendo ideias e o uso da língua materna – Simulado Encceja
- 50. Definição e propriedades da matéria – Simulado de Química
- 51. Diâmetro e escala – Simulado Encceja
- 52. Diminuição de custos e modernização – Simulado Encceja
- 53. Divisão de poder, Funai e recursos naturais – Simulado Encceja
- 54. Estado e Direito – Simulado Encceja
- 55. Estrangeirismo e memória cultural na Formação das Palavras
- 56. Evolução tecnológica, democracia e IDH – Simulado Encceja
- 57. Êxodo rural, desmatamento e trabalho infantil – Simulado Encceja
- 58. Expansão Marítima e Grandes Navegações: resumo com Simulado
- 59. Filósofos da Natureza – Resumo com Simulado Enem & Encceja
- 60. Frações e Sequências: resumo Encceja de Matemática com Simulado
- 61. Função de 1º Grau: resumo com exemplos e exercícios
- 62. Função do 1º Grau: resumo com Simulado Enem de Matemática
- 63. Gêneros Literários – Revisão Online com Simulado de Literatura
- 64. Homem, um animal político: veja o pensamento de Aristóteles
- 65. IDH, Cibercultura, e desigualdade: resumo de geografia
- 66. Impacto Ambiental: resumo com simulado de Geografia. Vem!
- 67. Indústria Cultural: resumo com Simulado Enem de Sociologia
- 68. Inscrições para o Encceja estão oficialmente abertas; veja como se inscrever
- 69. Interpretação de Textos e de Tirinhas – Resumo com Simulado
- 70. Interpretação em Inglês e Estatuto da Igualdade Racial – Simulado Encceja
- 71. Jean-Jacques Rousseau e o Iluminismo: resumo de filosofia
- 72. Juros Simples e Juros Compostos: Matemática Enem & Encceja
- 73. Leitura de gráficos e imagens: resumo com Simulado
- 74. Leitura de tabelas e probabilidade – Simulado Encceja
- 75. Linguagem Denotativa x Conotativa: resumo com simulado Enem
- 76. Línguas estrangeiras em nossa sociedade – Simulado Encceja
- 77. Lipídios na Biologia do Enem & do Encceja: resumo com Simulado Online
- 78. Lista de exercícios sobre equações do 1º grau: resumo e simulado
- 79. Lista de exercícios sobre hidrografia para o Enem
- 80. Literatura: veja desde a Carta de Pero Vaz de Caminha e até os dias de hoje
- 81. Lógica e Argumentação – Resumo de Matemática Encceja e Enem com Simulado
- 82. Massa, minerais e velocidade – Simulado Encceja
- 83. Média aritmética e paralelepípedo – Simulado Encceja
- 84. Média Simples e Média Ponderada: Resumo Enem & Encceja
- 85. Meiose – Resumo com Simulado de Biologia Enem & Encceja
- 86. Mercantilismo – Resumo com Simulado Enem de História
- 87. Métodos Contraceptivos e mais 10 Temas de Biologia Enem
- 88. Minorias, construção da sociedade e regionalismo – Simulado Encceja
- 89. Mitocôndria e Energia Celular: resumo Enem & Encceja de Biologia
- 90. Nada se cria, nada se perde, tudo se transforma: a Lei de Lavoisier
- 91. Números negativos – Simulado Encceja
- 92. O Átomo do Carbono – Resumo Enem com simulado de Química
- 93. O Cálculo de Porcentagem: resumo com Simulado de Matemática
- 94. O Mito da Caverna de Platão – Simulado de Filosofia
- 95. O Movimento de Rotação da Terra- Resumo Enem com Simulado
- 96. O que é a Filosofia – aula gratuita com Simulado Enem & Encceja
- 97. O Quinhentismo: resumo com simulado de Literatura Enem
- 98. O Romantismo na literatura brasileira: resumo com simulado
- 99. O Sistema Solar e a ordem dos planetas: resumo com simulado
- 100. O uso do Gerúndio – Resumo simulado Enem gratuito
- 101. Oração Subordinada: simulado Enem com resumo de Português
- 102. Os 4 Fusos Horários no Brasil: resumo de Geografia Enem
- 103. Os Filósofos do Iluminismo e a origem da Revolução Francesa
- 104. Os Filósofos Sofistas – Resumo com Simulado Enem & Encceja
- 105. Os seis Biomas Brasileiros: resumo de Geografia com Simulado Enem
- 106. Padronização estética, copa do mundo e interpretação – Simulado Encceja
- 107. Parnasianismo – Resumo com Simulado de Literatura
- 108. Placas Tectônicas: tsunamis, vulcões e terremotos: resumo Enem
- 109. Platão: o Mundo das Ideias e o Mundo dos Sentidos. Filosofia Enem
- 110. Prefixos e Sufixos – Resumo com Simulado Enem & Encceja de Gramática
- 111. Pronomes retos, oblíquos e demonstrativos: resumo com Simulado
- 112. Provas do Encceja: download grátis com gabarito
- 113. Queda Livre + MRU – Veja resumo com Simulado Enem & Encceja de Física
- 114. Regra de Três e Aresta: resumo com simulado Enem
- 115. Reprodução Assexuada – Resumo de Biologia Enem com Simulado
- 116. Resolução de questões de Circuitos Elétricos: Física Enem
- 117. Resumo com simulado de Acentuação Gráfica: Português Enem
- 118. Resumo com simulado de Regra de Três Simples, e Composta
- 119. Resumo da Revolução Francesa, com Simulado de História
- 120. Resumo de Divisão Silábica com simulado Enem de Português
- 121. Resumo de Física sobre Escalas Termométricas, com simulado
- 122. Resumo de Frações: Matemática com Simulado Enem
- 123. Resumo de Geologia Geral com simulado Enem de Geografia
- 124. Resumo de Hidrosfera, com Simulado de Geografia Enem
- 125. Resumo de Progressão Aritmética, com Simulado Enem
- 126. Resumo de Regra de Três: veja como resolver as questões no Enem e no Encceja
- 127. Resumo e Simulado sobre a filosofia de Aristóteles
- 128. Semana de Arte Moderna: literatura Enem. Resumo e Simulado
- 129. Simulado Encceja: testes rápidos de todas as matérias
- 130. Simulado Enem de Biologia – Os temas que mais caem
- 131. Sólido, Líquido, e Gasoso: resumo de Física Enem & Encceja, com Simulado!
- 132. Soma de Vetores – Resumo Online de Física com Simulado Gratuito
- 133. Substantivos: resumo de Português com simulado
- 134. Sustentabilidade, Lei Seca e gírias – Simulado Encceja
- 135. Tecnologia e Ciências em nosso cotidiano – Resumo e Simulado Encceja
- 136. Temas da Redação do Encceja confirmam Problemática Social
- 137. Terceira Geração Modernista – Resumo de Literatura com Simulado
- 138. Transporte marítimo e poluição nuclear – Simulado Encceja
- 139. Veja o Barroco em Portugal – Resumo com Simulado de Literatura
- 140. Veja o Movimento de Translação da Terra ao redor do Sol
- 141. Veja o que são as Proteínas: resumo de biologia Enem
- 142. Vida cotidiana e os impactos ambientais – Simulado Encceja
- 143. Vírus Ebola – Resumo Enem & Encceja com dicas e simulado online